作者：严芷涵 王学远 魏学哲 戴海峰
单位：同济大学汽车学院
引用本文：严芷涵, 王学远, 魏学哲, 等. 基于电化学阻抗谱几何解析的锂离子电池健康状态评估[J]. 储能科学与技术, 2025, 14(12): 4732-4742.
DOI：10.19799/j.cnki.2095-4239.2025.0635
本文亮点：1.提出了一种解析交流阻抗谱获取特征参数的几何方法 2.构建基于MLP的特征标准化模型和基于RF模型的电池SOH评估模型的电池SOH评估系统 3.针对不同频率范围的EIS数据选择合适的特征参数评估SOH
摘 要 锂离子电池(lithium-ion batteries, LIBs)的健康状态(state of health, SOH)评估对电动汽车(electric vehicles, EVs)和储能系统的安全性与经济性至关重要。针对传统SOH估计方法依赖全频段电化学阻抗谱(electrochemical impedance spectroscopy, EIS)数据、计算复杂度高且跨工况鲁棒性不足的问题，本研究提出了一种基于EIS几何解析与分段特征提取的锂离子电池SOH评估方法。通过弛豫时间分布(distribution of relaxation times, DRT)分析识别电池极化过程，构建分段等效电路模型(equivalent circuit model, ECM)，在高、中、低频段分别提取欧姆内阻(Ro)、电荷转移阻抗(charge transfer resistance, Rct)和扩散斜率(β)等9维特征参数，显著降低了数据存储与计算需求。为消除温度与荷电状态(state of charge, SOC)对特征参数的干扰，设计多层感知机(multilayer perceptron, MLP)模型将多工况特征映射至标准工况(25℃, 60% SOC)，并结合随机森林(random forest, RF)算法建立SOH预测模型。实验结果表明，该方法在多种工况下的SOH评估平均绝对误差(mean absolute error, MAE)和平均绝对百分比误差(mean absolute percentage error, MAPE)分别低至0.00662和0.251735%，优于梯度提升决策树(extreme gradient boosting, XGBoost)等对比算法。特征重要性分析显示，Rct、Ro和β对SOH预测的贡献显著，且单特征参数的独立评估误差仍低于0.42%，验证了该方法的工程适用性。本研究为嵌入式电池管理系统(battery management system, BMS)提供了高精度、低复杂度的SOH评估方案，尤其适用于有限硬件资源的实车应用场景。
关键词 锂离子电池；健康状态；电化学阻抗谱；几何解析；随机森林
随着全球能源结构的转型和碳中和目标的推进，电动汽车(EV)作为绿色交通的重要组成部分，正在快速普及。动力电池作为EV的核心能量来源，其性能和健康状况直接决定了整车的续航、安全性及经济性。近年来，锂离子电池(LIB)凭借其高能量密度、长循环寿命及无记忆效应等优势，已成为主流的电化学储能技术路线。在众多正极材料体系中，磷酸铁锂(LFP)电池因其优异的热稳定性、本征安全性及成本优势，在动力与储能场景中获得广泛应用。特别是高容量LFP电芯的广泛采用，不仅有助于提升系统整体能量密度，还可通过减少并联电芯数量以简化系统拓扑结构，降低总连接电阻与模组数量，从而减少对电压、电流等传感器的依赖，有助于提高系统的集成效率与可靠性。
为了确保电池系统在全生命周期内的安全与高效运行，现代电池管理系统(BMS)被广泛部署于动力电池包中，负责实时监测和调控电池的运行状态。其中，电池健康状态(state of health, SOH)作为衡量电池性能衰退程度的关键指标，是实现预测性维护、生命周期管理和残值评估的重要基础。传统SOH估计方法通常依赖采集电流、电压、温度和内阻等传感器数据，基于统计回归、机器学习或电化学建模等手段对其进行特征提取与建模，从而建立SOH估计模型。
目前常见的电池数据源主要包括充放电曲线数据、短时脉冲响应数据和电化学阻抗谱(EIS)等。文献[19]提出基于电压-容量曲线与微分容量(IC)分析提取退化特征以估计SOH，虽然该方法具有一定的物理意义，但电压信号本身易受测量噪声干扰，IC曲线对信号微小扰动高度敏感，导致该方法在工程应用中稳定性较差。文献[20]采用卷积神经网络(CNN)对电池电压曲线实现自动特征提取与SOH预测，具备较强的端到端建模能力，并在不同老化场景下表现出良好的泛化性。但该方法在不同电池型号及化学体系上的有效性尚未得到验证，这限制了其在跨平台、跨应用场景中的实际部署价值。文献[21]则基于混合脉冲功率特性(HPPC)测试，采用最小二乘法拟合等效电路模型(ECM)参数，并构建热-电耦合模型以研究不同温度与荷电状态(SOC)条件下的参数变化。然而，该方法并未将所提取的ECM参数进一步用于SOH估计，因此其在实际健康评估中的有效性尚待验证。
相较于传统电压、电流等时域信号，电化学阻抗谱(EIS)作为一种非侵入、非破坏、信息密度高的频域表征手段，近年来在动力电池老化分析与健康评估中得到广泛关注。EIS不仅能够揭示电池在各频域下的动力学响应特性，还可通过与等效电路模型结合提取具有物理意义的参数，如欧姆内阻、电荷转移阻抗、双电层电容等。已有多项研究尝试利用EIS特征进行SOH估计，例如文献[24]提取6个多频静态阻抗特征，并通过鲸鱼优化算法-反向传播(WOA-BP)神经网络建立SOH估计模型。但该方法未考虑温度对EIS的显著影响，导致其在跨温度应用中鲁棒性较差。文献[25]提出基于弛豫时间分布(DRT)域的SOH估计框架，选取8个时间常数相关特征用于建模，但其验证仅限于25 ℃与100% SOC工况，适应性有限。文献[26]通过结合改进的ECM与高斯过程回归(GPR)模型刻画电池在不同温度下的老化模式，具有一定泛化能力，但对其他电化学过程的适用性仍存在疑问。此外，文献[27]通过在不同测试系统与噪声水平下构建鲁棒的EIS-SOH映射关系，证明了频域建模的潜力，然而其对宽频率采样的依赖性较高，制约了其在嵌入式BMS中的工程可行性。
与直接利用原始EIS数据相比，基于ECM建模提取的参数具有更高的可解释性与工程可实施性，能够更有效地反映不同电化学过程及老化机制，在实际BMS系统中具有更大的部署潜力。目前主流的ECM参数辨识方法仍以非线性最小二乘(NLS)为核心，辅以粒子群优化(PSO)、遗传算法(GA)等元启发式算法以提高全局最优性。但这些方法普遍存在计算复杂度高、参数初始化依赖性强、易陷入局部最优等问题，限制了其在多工况下的泛化与实时性表现。
针对以上问题，本研究提出一种基于电化学阻抗谱的几何解析健康特征提取方法。该方法融合等效电路建模与弛豫时间分布(DRT)分析，构建分段线性拟合框架，在兼顾拟合精度的同时显著降低计算复杂度与存储开销。为提升模型在非标准测试条件下的适用性，进一步引入多层感知机(MLP)神经网络对不同温度与SOC下的EIS特征进行归一化与标准化处理。通过特征选择与相关性分析，最终实现了在多温度、多工况下对锂离子电池SOH的精准、高鲁棒性估计。本研究为EIS在实际BMS系统中的部署提供了高效、可解释的技术路径，对提升电池健康评估的可靠性与智能化水平具有重要意义。
1 实验对象与设计
1.1实验对象
本次实验选取湖北亿纬动力有限公司生产的型号为LF50F的方形铝壳磷酸铁锂电池作为实验对象。
1.2实验设计
冬烨恒温箱温度设置为25℃，新威CT-8008-5V50A-NTFA电池测试仪对电池进行0.5C倍率恒流恒压充电、1C倍率恒流放电，充放电循环40次为一个循环周期，放电截止电压为2.5 V，充电截止电压为3.65 V，将每个周期最后一次放电容量作为电池的当前容量。
在每次循环充放电周期结束之后，在不同温度(-5℃、10℃、25℃、35℃)、不同荷电状态(20%、40%、60%、80%)下使用东华DH7007阻抗测试仪对电池进行阻抗测试，其中激励电流为3 A，采样频率范围为10 kHz~0.01 Hz，在频率每十进制间隔内，以对数尺度均匀离散化，每个间隔采集10个点。
2 基于EIS的等效电路模型
2.1SOH定义
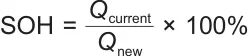
SOH反映的是电池老化状态和性能的关键指标，用百分比表示。将电池容量作为研究对象，通过容量变化来反映电池当前的老化状态，是目前使用较为广泛的定义。本研究使用的也是该定义，即
 |
(1) |
式中，Qcurrent是电池当前可用最大容量；Qnew为电池出厂时的最大容量。
2.2阻抗复平面的阻抗模型
电化学阻抗谱在阻抗复平面的几何表现形式通常为若干半圆和一条近似与横轴成45°的斜线，大容量磷酸铁锂电池测得的EIS只有一个明显的圆弧，如图1(a)~(d)所示。这是因为电池内部极化反应的多样性及复杂性，半圆呈现出相互交叠的现象，无法依据阻抗复平面图判断极化反应个数。而弛豫时间分布(DRT)方法无须依赖先验知识或预设等效电路模型，即可将EIS谱图中高度重叠的多个极化过程分辨开，从而达到识别体系极化过程数量和极化电阻大小的目的。如图1(e)~(h)所示，对不同温度下的EIS进行DRT分析，阻抗峰P1、P2分别归属于SEI膜阻抗和电荷转移阻抗，阻抗峰P3~P5均归属于固相扩散阻抗。低温时，反应动力学活化能壁垒升高，电解液离子电导率下降，电荷转移阻抗急剧增大，主导了该温度下的电池极化过程。特征峰P1和P2的时间常数满足log(τsei/τct)<1时，SEI膜形成与电荷转移过程的时间常数耦合，导致阻抗复平面的圆弧合并。
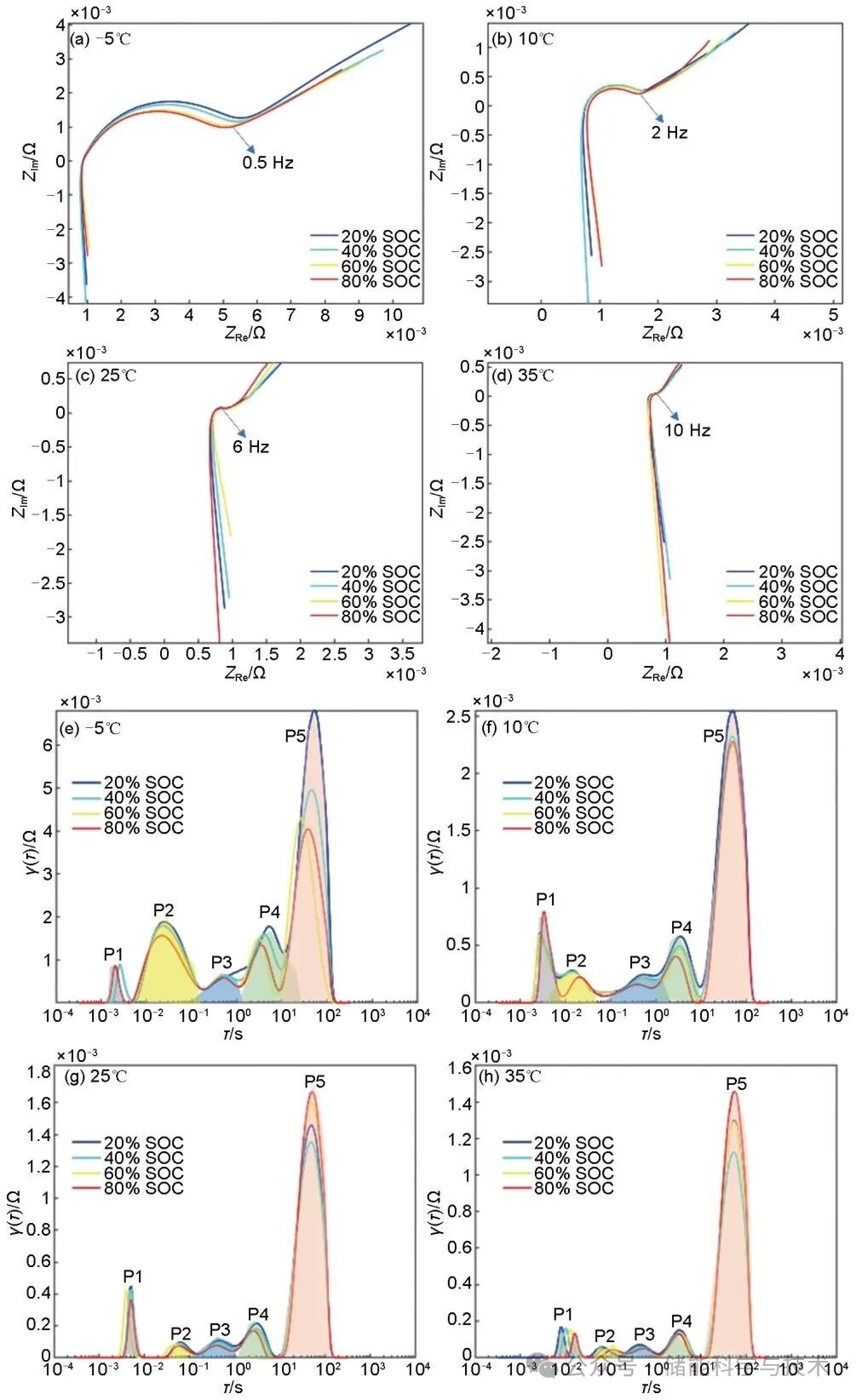
图1 EIS曲线和DRT曲线
基于上述DRT分析结果，构建等效电路模型(RL)R(RQ)W描述EIS，两者的频响特性一一对应，如图2所示。其中黄色曲线对应阻抗谱的高频段，是导线中电子运动和内部电极交互所产生的感应效应，由于高频段EIS发生逆时针偏角，因此用电阻与电感并联的复合元件R∥L表示该特性。EIS与实轴的交点为金属固相中电子与电解液相中离子运动形成的欧姆电阻，用电阻Ro表示。蓝色曲线对应阻抗谱的中频段，该阶段描述了锂离子通过固体电解质薄膜(solid electrolyte interphase, SEI)扩散，从电解质到电极表面、电极本体活性材料的过程，以电荷转移过程为主导，用电阻与常相位元件(CPE)并联的复合元件R∥Q表示。绿色曲线对应阻抗谱的低频段，描述了离子在电解质中的扩散现象，用Warburg元件表示。
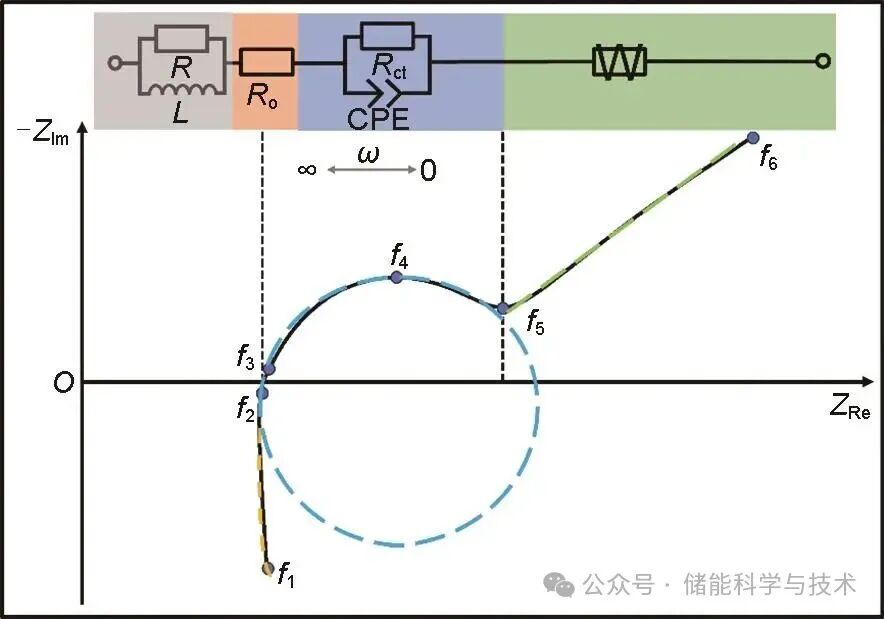
图2 基于EIS的等效电路模型
3 基于EIS几何解析法的特征参数辨识
受实车嵌入式系统硬件资源的约束，测试平台仅能支持有限频率范围的激励信号生成与采集，无法覆盖EIS理论所需的0.01 Hz~1 MHz全频率范围。因此，本研究对EIS进行频率范围划分，在不同频段提取特征参数。
如图3所示，将阻抗谱在频域尺度下划分为多个子区间，f1、f2、f3、f4、f5、f6分别为高频、中频、低频阶段的起始和终止采样频率。
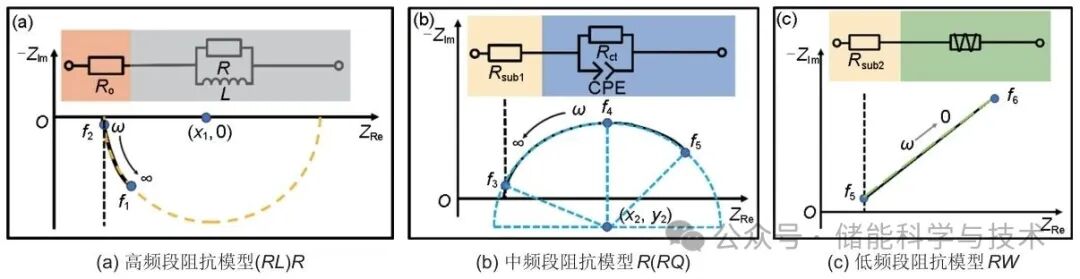
图3 基于EIS的分频等效电路模型
3.1高频段特征参数提取
高频感抗阶段与LIBs本身无关，不提供有关电池电化学状态的有价值信息，通常对该阶段的数据进行裁剪，但基于该段EIS可辨识出阻抗谱与实轴的交点，即欧姆内阻Ro，构建如图3(a)所示的高频段阻抗模型(RL)R，阻抗表达式如下：
 |
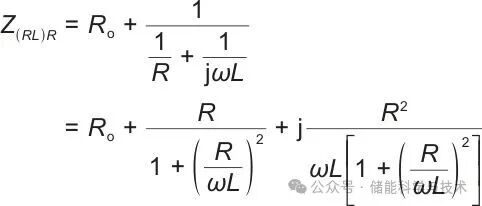(2) |
式中，ω为角频率。
式(2)经变换得如下表达式：
 |
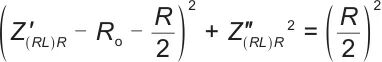(3) |
式中，Z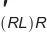
和
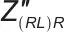分别为高频段阻抗模型(RL)R的阻抗实部和虚部。
按照该方程作图可得一个圆，在阻抗复平面中为第四象限中的圆弧，称为感抗弧，如图3(a)所示。基于式(3)建立隐式方程：
 |
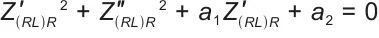(4) |
式中，a1、a2为待求的系数。
遵循最小二乘法，所有阻抗复平面的点到拟合圆的距离平方和最小的准则，将求解非线性回归问题转化为求解线性方程组问题，避免优化参数陷入局部最小值的窘况。基于极值原理建立法方程：
 |
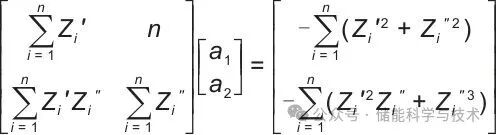(5) |
式中，Z
和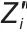
分别为高频段EIS各阻抗的实部和虚部。
由系数a1、a2构成的多项式可求得特征参数R、Ro、L。
3.2中频段特征参数提取
将高频段阻抗模型(RL)R简化为电阻Rsub1，构建如图3(b)所示的中频段阻抗模型R(RQ)，阻抗表达式如下：
 |
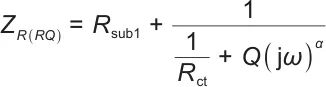(6) |
式中，Rct为电荷转移阻抗；Q为常相位元件CPE的计算参数；α为常相位元件CPE的无量纲指数。
式(6)经变换得如下表达式：
 |
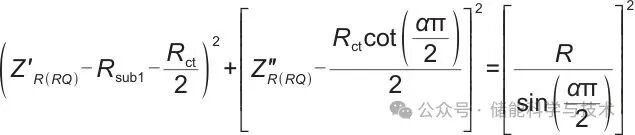(7) |
式中，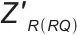
和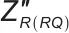
分别为中频段阻抗模型R(RQ)的阻抗实部和虚部。
按照该方程作图可得一个圆，在阻抗复平面中为圆心在第四象限、轨迹在第一象限的圆弧，如图3(b)所示，获取特征参数的方法与高频段方法一致，得到特征参数Rsub1、Rct、α、Q，其中Rsub1数值上与阻抗复平面中的阻抗谱与实轴的交点(即欧姆内阻)等同。
3.3低频段特征参数提取
高频对Warburg元件影响较小，高频和中频阶段的阻抗可简化为电阻Rsub2，构建如图3(c)所示的低频段阻抗模型RW，阻抗表达式如下：
 |
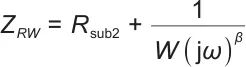(8) |
式中，W为Warburg元件的计算参数；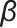
为Warburg元件的无量纲指数。
RW在阻抗复平面表示为一条斜率为tan(βπ/2)，与实轴相交于(Rsub2,0)的直线，如图3(c)所示。对低频段EIS线性拟合，得到特征参数β和W。
4 电池SOH评估系统构建
4.1基于多层感知机的特征标准化模型
由图1(a)~(d)可知，在同一老化阶段下，温度对EIS的影响较大，SOC对EIS的影响相对较小但不可忽视，因此在训练SOH评估模型之前需要对不同工况下的EIS标准化。基于上述几何解析法辨识得到不同温度、荷电状态、老化阶段下R、Ro、Rsub1、L、Rct、α、Q、β、W共9个特征参数，用这些特征参数表征不同工况下的EIS，本研究内容将T为25℃、SOC为60%定义为标准工况(标况)条件。
建立特征标准化模型旨在消除工况差异(T和SOC)对特征参数的影响，将不同老化阶段下采集的特征统一映射为标准工况下的可比数值，因此构建基于多层感知机的特征标准化模型。
多层感知机是一种监督学习算法，通过多层神经元和非线性激活函数学习输入到输出的复杂映射。相较于其他算法，它拥有强大的非线性拟合和特征自动组合的能力。在特征标准化模型构建中，该方法能够精准学习T、SOC与EIS特征参数间的非线性耦合关系，实现跨工况的物理量统一校准，而传统线性方法(如多项式回归)难以捕捉此类复杂依赖。
对每一个特征参数xi建立一个具有2个隐藏层的多层感知机，构建特征映射模型，如图4所示。输入层维度为6，对应关于T和SOC的二阶多项式各项；输出层维度为1，对应当前工况下的特征参数xi修正到标准工况下的xistd的补偿量Δxipred=xistd,pred - ximeas,pred，xistd,pred为标况下特征参数xi的评估值，ximeas,pred为当前工况下特征参数xi的评估值；隐藏层1和2分别包含64个和32个神经元，输入层到第一隐藏层、第一隐藏层到第二隐藏层、第二隐藏层到输出层的权重分别为Win、Wh1、Wout，第一隐藏层、第二隐藏层、输出层的偏置分别为bh1、bh2、bout。MLP采用自适应矩估计(Adam)优化器，根据损失函数梯度更新MLP参数，损失函数为Δximeas和Δxipred的均方根误差，Δximeas为当前工况与标准工况下特征参数xi的差值。
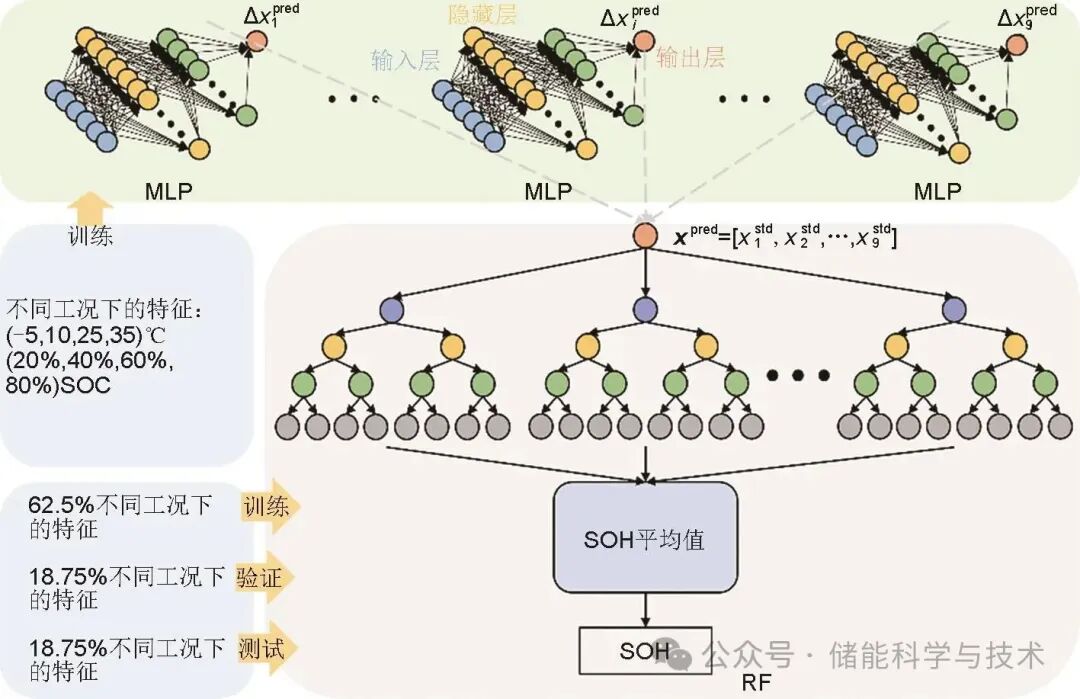
图4 SOH评估系统
为充分捕捉T与SOC对EIS特征参数的交互影响，首先对T和SOC进行二阶多项式扩展。将2维输入向量[T SOC]T转换为6维特征空间，如下所示：
 |
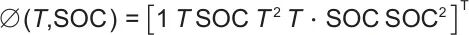(9) |
单层神经网络的前向传播计算表达式如下：
 |
(10) |
式中，a为上一层的输出向量；W为权重矩阵；b为偏置向量。
MLP最终的输出表达式如下：
 |
(11) |
Δxipred反映了工况变化引入的特征偏移量，将当前工况下特征参数真实值与该偏移量相加，即得到标准化后的特征值xistd，表达式如下所示：
 |
(12) |
式中，xistd为标准化后的特征值；ximeas为当前工况下特征参数的真实值。
4.2基于随机森林的电池SOH预测模型
随机森林回归是一种集成学习方法，通过构建多棵决策树并综合其评估结果来进行回归评估，因此选择采用随机森林回归算法构建电池SOH评估模型，通过集成学习框架建立标准工况下的EIS特征与电池容量衰减之间的非线性映射关系。如图4所示，模型以前期经过标准化处理的9维EIS特征作为输入，经过随机森林回归计算后输出SOH评估值。
采用N棵决策树，每棵树基于随机抽取的训练子集和随机选择的特征子集独立构建。在节点分裂时，算法从候选特征中寻找使均方误差(mean square error, MSE)下降最大的划分点，递归构建二叉树结构直至满足停止条件。通过双重随机性机制(数据随机采样和特征随机选择)可以有效提高模型的泛化能力，同时自动捕捉特征间的非线性关系。最终评估结果为所有决策树输出的平均值，SOH评估公式如下：
 |
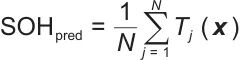(13) |
其中，N是树的数量，由于样本较少，本模型取值为50；Tj(x)是第j棵决策树的评估结果；x是标准化后的EIS特征向量。
5 实验数据处理与结果分析
5.1标准状况下特征参数与SOH的相关性分析
图5展示了25℃、60%SOC的标准工况下9个特征参数与SOH的皮尔逊相关系数。其中Rsub1、欧姆内阻(Ro)与电荷转移阻抗(Rct)分别呈现-0.80944、-0.78726和-0.62038的负相关性，反映了电池内部导电网络退化和电极界面电荷转移阻力增大现象。扩散相关参数(β和W)的负相关性(-0.35955和-0.1761)说明锂离子固相扩散能力随容量衰减而下降。而常相位元件参数(α和Q)的相关性(-0.51087和-0.1639)与Ro、Rct相比，与老化机制的关联性较弱。该结果验证了分段ECM模型提取的特征参数具有明确的物理意义，其中Rct、Ro可作为SOH评估的核心指标。
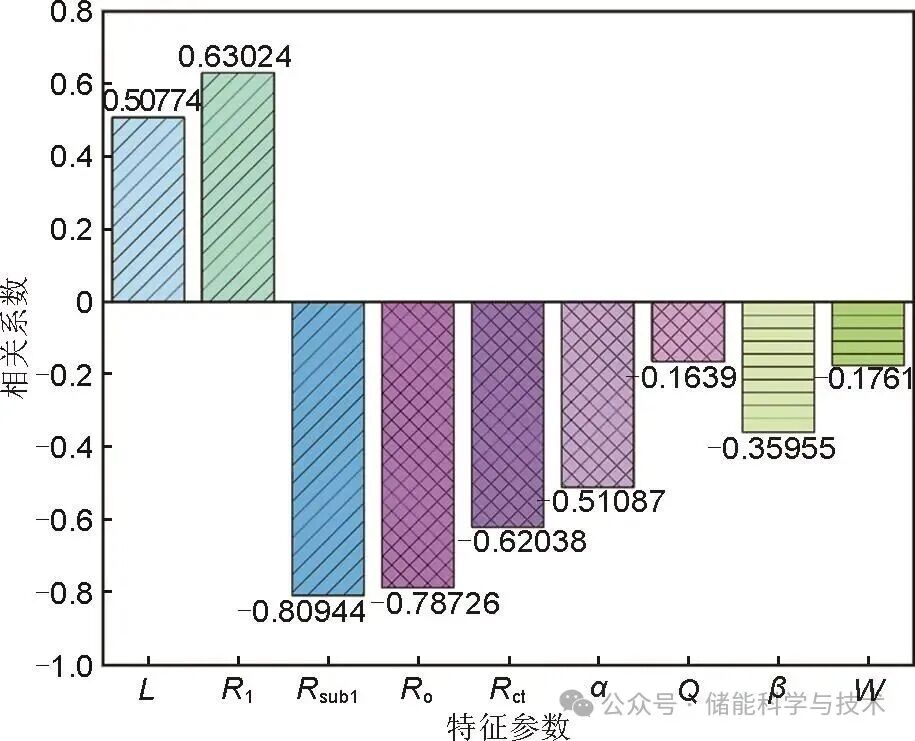
图5 特征参数与SOH的皮尔逊相关系数
5.2SOH评估系统分析
采用MAE、MSE与MAPE来评价动力电池健康状态的评估结果，3个指标的计算公式如下：
 |
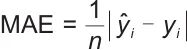(14) |
 |
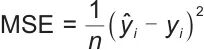(15) |
 |
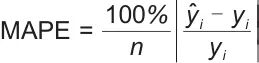(16) |
将上文提到的几何解析法提取出的不同工况下的9种特征参数输入电池SOH评估系统训练模型，如图6(a)所示，特征标准化模型和SOH评估模型各自单独训练。
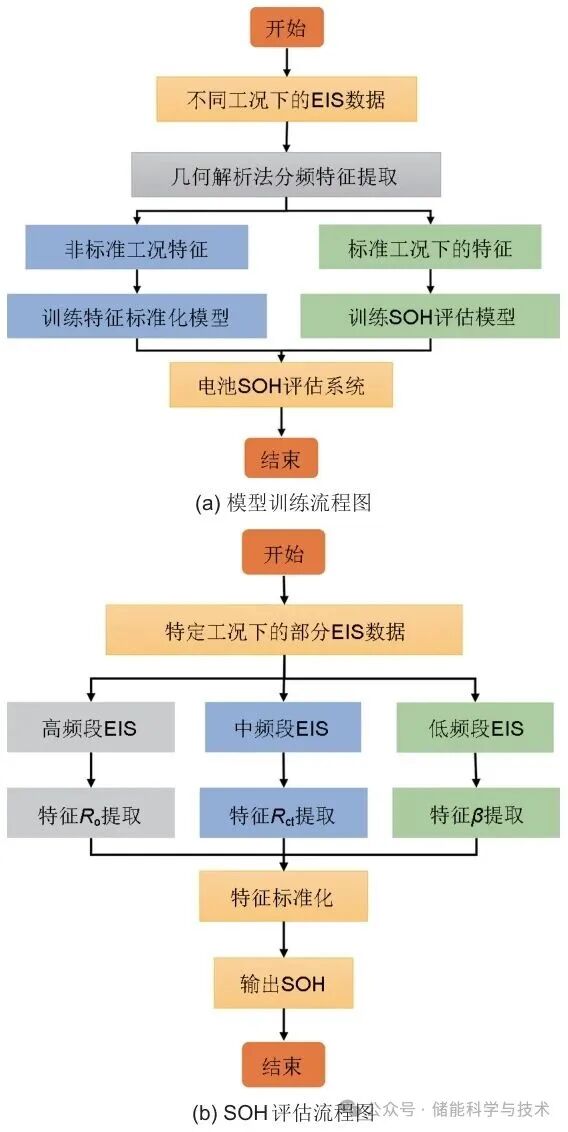
图6 模型训练流程图
其中，MLP模型与特征标准化的协同工作机制通过分阶段建模实现了跨工况的稳定评估。利用MLP学习工况变量T和SOC对EIS参数的非线性影响，再通过特征标准化将任意工况下的测量值映射到标准参考工况，从而消除工况干扰。其中T和SOC的多项式向量作为输入集，特征xi作为不同MLP模型的输出集，对模型进行训练。在此基础上继续完成特征标准化，MLP评估的差值Δxipred量化了工况变化引起的参数偏移，通过将该差值叠加到原始测量值上，即可获得相当于在标准工况下测得的校正值，最终完成模型的建立。为了验证模型的有效性，如图6(b)所示，结合训练后的基于随机森林的SOH评估模型，计算得到所有工况下SOH评估值与SOH真实值的平均相对误差为1.2104%，最大相对误差为2.7974%，没有出现SOH评估异常的偏差值，验证了模型的准确性。
近期研究表明，EIS结合机器学习在SOH评估中具有显著潜力。文献[28]指出，基于XGBoost的方法仅需少量特征即可实现90%的预测精度，尤其适合嵌入式BMS应用。相较于该研究仅验证单一模型，本研究进一步系统对比了梯度提升决策树(extreme gradient boosting, XGBoost)与随机森林及线性模型在本实验条件下的性能差异。如图7所示，通过将数据集按10∶3∶3的比例划分为训练集、验证集和测试集，本研究比较了XGBoost和随机森林在不同数据集上的表现。XGBoost在训练集上表现出极高的拟合精度(R2 = 0.9991)，然而在验证集(R2 = 0.7683)和测试集(R2 = 0.8739)上的性能明显下降，表现出一定的过拟合风险。相比之下，随机森林在各个数据集上都保持了较为稳定的表现，训练集(R2 = 0.9774)、验证集(R2 = 0.8555)和测试集(R2 = 0.8981)的预测精度较为一致，且在泛化能力上明显优于XGBoost。考虑到XGBoost的过拟合问题和较大的性能波动，最终选择随机森林作为本研究的最佳模型，因为它在保证较高精度的同时，具备更强的稳定性和泛化能力。
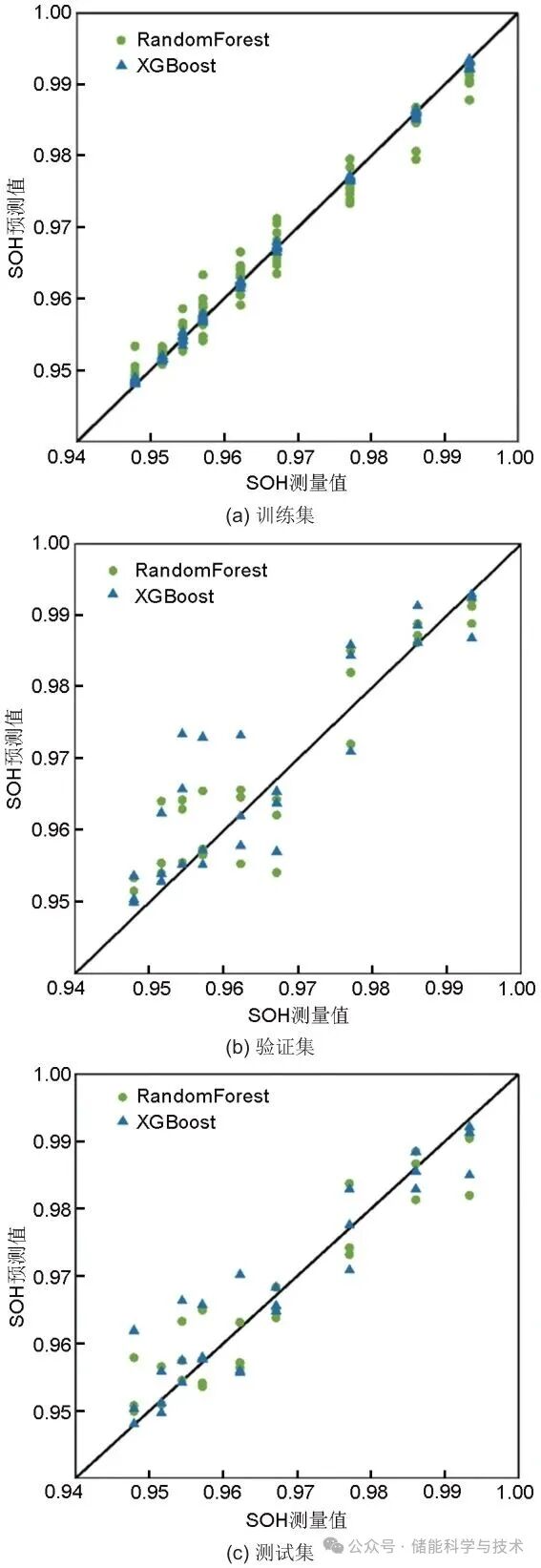
图7 SOH测量值和预测值的对比
通过特征重要性评估量化各EIS特征对SOH评估的贡献度，如图8所示，特征参数Rct、Ro、Rsub1、β均大于0.1，因此这4个特征参数为强相关特征。Ro、Rsub1和Rct、β为基于高频段、中频段、低频段EIS获得的特征参数，由于Ro、Rsub1、Rct随着电池老化而变大，扩散阶段的斜线斜率(变化趋势与β等同)会随着电池老化呈现减小的趋势，因此重要性评估结果符合一般性规律。
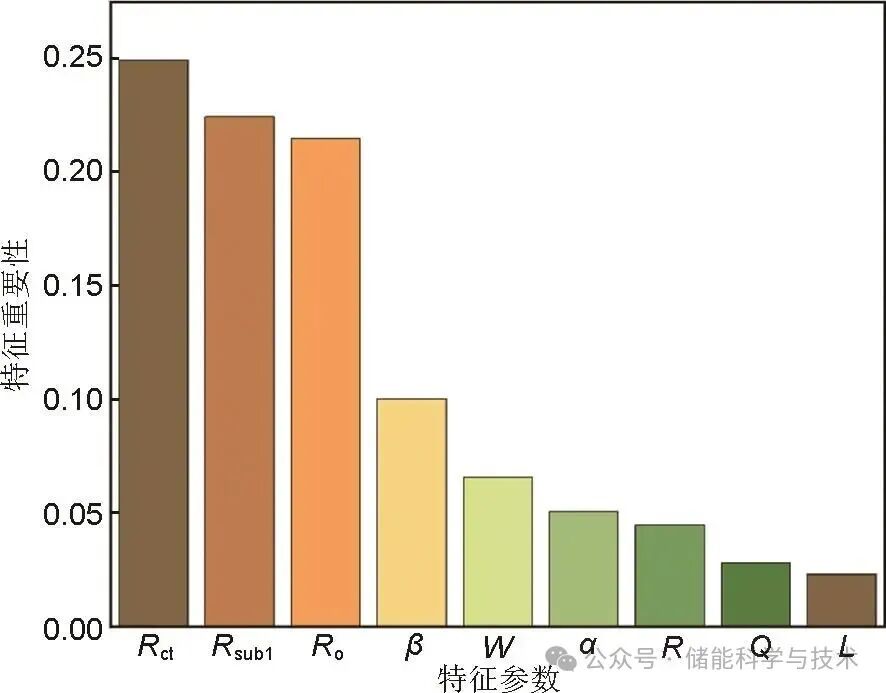
图8 EIS特征参数重要性对比
将上述Ro、Rsub1、Rct、β和所有特征分别作为电池SOH评估系统的特征输入模型，计算得到的SOH评估值和SOH真实值对比如图9所示。如表1所示，对评估的结果进行量化。从表中结果可以看出，基于Ro的评估效果优于Rsub1。虽然这4个单特征参数对SOH的敏感程度不一样，但是彼此的误差分析差距并不大，因此均可以作为电池健康参数实现SOH的高精度评估。
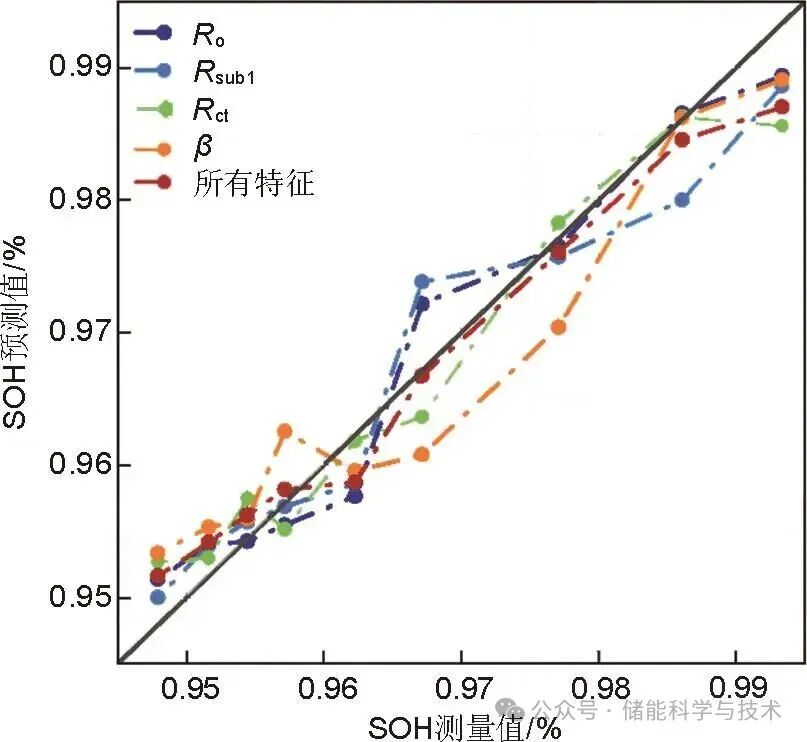
图9 EIS不同特征参数下SOH测量值和评估值对比
表1 基于不同特征参数的SOH预测结果
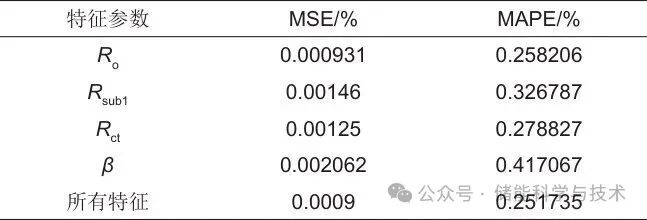
考虑到不同的实车嵌入式系统硬件条件，如果测得频率范围处于EIS高频阶段，则选择Ro作为健康特征参数；如果测得频率范围处于EIS中频阶段，则选择Rct作为健康特征参数；如果测得频率范围处于EIS低频阶段，则选择β作为健康特征参数。这样既减少了数据存储，又保证了SOH评估精度。
6 结 论
针对实车阻抗测试数据量不足和不同工况下电池SOH不一致等问题，本研究提出了一种解析交流阻抗谱获取特征参数的几何方法，构建了基于MLP的特征标准化模型和基于RF模型的SOH评估模型的电池SOH评估系统。将不同工况下辨识得到的9种特征参数输入SOH评估系统，SOH评估结果的MSE和MAPE分别为0.0009%和0.251735%，证明了基于该几何解析方法辨识特征参数的可行性。对比基于RF算法和XGBoost算法构建的SOH评估模型，SOH评估结果表明RF算法具有泛化稳健和可解释性等优势。将4种单特征参数作为SOH评估系统的输入，SOH评估结果整体趋势均与实际SOH一致，且MSE和MAPE数值分别小于0.0021%和0.42%。针对不同频率范围的EIS数据选择合适的特征参数评估SOH，说明该方法在实际车载BMS中具有应用价值。
第一作者：严芷涵（1999—），女，硕士研究生，研究方向为动力电池健康状态评估；
通讯作者：王学远，预聘助理教授，研究方向为锂离子电池管理。
发表评论