作者：谭金龙1 陈军2 赵启2 崔大林3 刘永强2 张路2
单位：1. 重庆大学，输配电装备及系统安全与新技术国家重点实验室；2. 国网新疆电力有限公司电力科学研究院；3. 国网新疆电力有限公司
引用本文：谭金龙, 陈军, 赵启, 等. 基于改进型双重深度确定性策略梯度与自适应分布式模型预测控制融合的电网侧储能系统协同优化方法[J]. 储能科学与技术, 2025, 14(11): 4289-4299.
DOI：10.19799/j.cnki.2095-4239.2025.0473
本文亮点：本文融合增强DDPG算法和自适应DMPC方法提出了一种自适应储能优化策略。该策略充分利用DDPG在处理高维连续动作空间方面的优势和MPC在处理系统约束和预测未来状态方面的能力，有效应对可再生能源并网带来的不确定性和复杂性。仿真结果表明，该方法在优化存储容量分配、系统运行成本和可再生能源消耗率方面取得了显著改善。特别是在高渗透率的情况下，所提出的方法在可再生能源消耗率方面的优势更加明显。未来的研究可以扩展到更广泛的能源系统，如热、天然气和其他多能源互补系统。
摘 要 为应对可再生能源并网给电网侧带来的不确定性与复杂性，解决电网侧储能系统在容量分配、运行成本及能源消纳等方面的问题，提升电网稳定性与能源消纳效率，本文融合改进的深度确定性策略梯度(deep deterministic policy gradient，DDPG)算法与自适应分布式模型预测控制(distributed model predictive control，DMPC)方法，提出电网侧储能系统自适应协同优化策略。改进DDPG引入偏好体验回放和噪声调整机制以增强学习效率与探索能力，自适应DMPC通过分解大规模问题实现并行计算与局部优化。测试表明，相较于传统 DDPG 算法，该策略在电网侧储能容量分配优化、降低系统运行成本及提高可再生能源消纳率等方面效果显著。该策略为电网侧可再生能源储能系统的优化分配提供了创新解决方案，对保障电网稳定运行具有重要意义。
关键词 储能系统；协同优化；可再生能源集成；深度强化学习；模型预测控制；自适应控制
随着全球对清洁能源的需求日益增长，可再生能源如太阳能、风能等得到了广泛的开发和利用。然而，可再生能源具有间歇性、波动性等特点，这给电力系统的稳定运行带来了巨大挑战。这种不确定性使得电力系统的供需平衡难以维持，容易导致电网频率波动、电压不稳定等问题。储能系统可以作为一种缓冲装置，调节可再生能源的输出，使其更加平稳地接入电网。然而，要充分发挥储能系统的作用，需要对其充放电策略进行优化，以适应可再生能源的不确定性。
近年来，深度强化学习技术凭借其在解决复杂优化问题方面的强大能力，在能源领域备受关注。深度确定性策略梯度(deep deterministic policy gradient，DDPG)算法作为深度强化学习中的重要算法，在连续动作空间的决策问题中取得了一定成果。它通过结合深度神经网络和确定性策略梯度，能够从高维状态空间中学习到有效的控制策略。但在储能系统优化应用中，传统DDPG算法存在学习效率低、易陷入局部最优解等问题。为克服这些问题，改进型双重深度确定性策略梯度算法应运而生。其通过引入双重网络结构和优化技巧，显著提升了算法的收敛速度与稳定性。不过，面对可再生多能源储能系统中高维、复杂的决策环境，单一的深度强化学习算法仍存在局限性。
与此同时，分布式模型预测控制(distributed model predictive control，DMPC)在能源系统优化控制中展现出独特优势。DMPC将大规模系统分解为多个子系统，各子系统在考虑自身动态约束的同时，通过信息交互协同优化，有效提高了系统的鲁棒性和适应性。在处理可再生能源的不确定性和系统动态变化方面，DMPC能够基于预测模型滚动优化控制策略，实时调整系统运行状态。然而，传统DMPC在模型准确性和计算效率上仍需进一步提升，尤其是在多能源耦合的复杂场景下，其难以充分挖掘系统潜力。
目前，深度强化学习和DMPC集成在可再生多能源储能优化集成策略中的分析仍然不足。在储能系统的优化管理领域，已有诸多研究探索不同的技术路径。文献[13]提出一种结合电池和超级电容器的混合储能系统，有效平滑了风电输出功率的波动，提高了系统的经济性和可靠性，但未充分考虑储能系统的长期优化。文献[14]从多目标优化角度讨论了电力和天然气系统的协同规划策略，为可再生能源的有效利用提供了新思路。文献[15]引入大数据技术分析电力消耗行为，提升了需求侧管理的准确性和效率，文献[16]将其扩展到冷热电联产系统，并提出了基于模型的预测控制能量管理和控制策略。然而，上述研究在处理高维和高复杂性的能源系统优化问题时仍面临挑战。文献[17]对电-热-气多能源系统的优化运行模型和算法进行全面综述，为后续研究提供重要理论支持。在深度强化学习方面，文献[18]指出深度Q网络在解决大规模状态空间问题方面具有显著优势，文献[19]提出的DDPG算法可有效处理连续动作空间中的控制问题，这些为解决可再生多能源存储优化集成策略中的高维决策空间问题提供了有力工具。
本工作关注可再生多能源储能系统的集成策略，提出一种将DDPG和DMPC相结合的创新方法，旨在提高系统的整体效率和可靠性。该方法通过深度强化学习技术优化能源调度决策，同时使用分布式控制架构来提高系统的鲁棒性和适应性。研究采用多目标粒子群优化算法平衡系统经济性、环境影响和可靠性等多个目标，有效解决传统优化方法在处理复杂和动态能源系统时的局限性问题。此外，引入集成学习算法，提高能源需求预测的准确性和可靠性，为优化决策提供更准确的输入。通过实证分析，验证了本工作所提出的方法在不同操作条件下的有效性。结果表明，该方法可以显著提高系统的整体性能，包括降低运营成本、减少碳排放和提高能源利用率。
1 储能系统集成建模
构建可再生能源并网储能系统的数学模型是设计最优控制策略的基础。该系统由一个由锂电池、超级电容器和储热装置组成的混合储能单元，以及一个风电场和一个光伏发电厂组成。系统的动态行为可以用状态空间方程来描述：
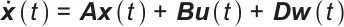 | (1) |
式中，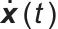
表示t时刻状态向量x(t)的一阶导数；A表示系统矩阵；x(t)表示t时刻的状态向量，包含储能单元充电状态、可再生能源输出等关键系统状态信息，
是状态向量，包含储能单元的充电状态和可再生能源输出，其中Ebat表示储能电池的能量状态，Esc表示超级电容器的能量状态，Eth表示热储能的能量状态，Pwt表示风机的输出功率，Ppv表示光伏的输出功率；B表示输入矩阵，体现控制输入向量u(t)对状态向量x(t)变化的影响关系；u(t)表示t时刻的控制输入向量，
是控制输入向量，其中
表示电池的充/放电功率，
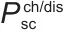表示超级电容器的充/放电功率，
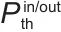表示热储能的输入/输出功率；D表示扰动输入矩阵，描述随机扰动向量w(t)对状态向量x(t)变化的作用；w(t)表示t时刻的随机扰动向量，代表风机输出等随机、不确定的干扰因素，会使系统状态偏离预期变化。
进一步，建立随机扰动向量的微分方程：
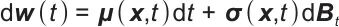 | (2) |
式中，dw(t)表示随机扰动向量w(t)的微分形式；μ(x,t)表示漂移系数(也称趋势系数)，是关于状态x和时间t的函数；σ(x,t)表示扩散系数，是关于状态x和时间t的函数；dBt表示布朗运动(维纳过程)的微分形式，是随机微分方程里描述随机扰动的核心元素，体现随机、无规则的扰动特性，用于模拟如风机出力随机波动这类现象。
为了在多个时间尺度上描绘动态耦合效应，建立了一个三能级能量流方程。毫秒级超级电容器动力学可以表示为：
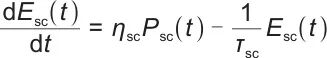 | (3) |
式中，Psc(t)表示t时刻超级电容器的功率；ηsc表示超级电容器的效率系数；τsc表示超级电容器的时间常数；dEsc(t)/dt表示t时刻超级电容器能量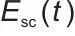
的变化率。
进一步，分钟级电池的动态方程为：
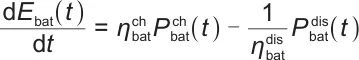 | (4) |
式中，Ebat(t)表示电池在时刻t的能量状态；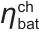
表示电池的充电效率；
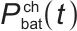表示时刻t电池的充电功率；
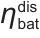表示电池的放电效率；
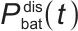表示时刻t电池的放电功率；dEbat(t)/dt表示电池能量Ebat(t)随时间t的变化率，即能量的动态变化速率，由充电、放电功率及效率共同决定。
每小时储热的动态可以描述为：
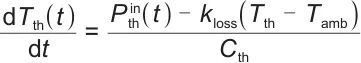 | (5) |
式中，Tth(t)表示时刻t热储能的温度；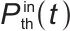
表示时刻t热储能的输入功率；kloss表示热储能的热损失系数；Tamb表示环境温度；Cth表示热储能的热容；dTth(t)/dt表示热储能温度Tth(t)随时间t的变化率，即温度动态变化速率，由输入功率、热损失及热容共同决定。
电网侧功率平衡约束表示为：
 | (6) |
式中，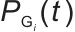
表示时刻t第i个常规发电单元向系统注入的功率；ΩG表示常规发电单元的集合，下标
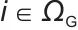表示对集合内所有常规发电单元进行求和运算；
表示时刻t第j个可再生能源发电单元的输出功率；ΩRES表示可再生能源发电单元的集合，下标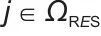
表示对集合内所有可再生能源发电单元进行求和运算；
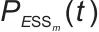表示时刻t第m个储能装置的功率交互量(储能装置含锂电池、超级电容器、储热装置等，通过电-热/电转换参与电网功率交互，充电时为负、放电时为正)；ΩESS表示储能装置集合，下标
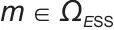表示对集合内所有储能装置进行求和运算；
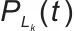表示时刻t第k个负荷的消耗功率，是电网中各类用电设备从系统中取用的功率；ΩL表示负荷的集合，下标
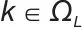表示对集合内所有负荷进行求和运算；Ploss(t)表示时刻t电网的功率损耗，即电能在传输、转换等环节中损失的功率。
总体系统优化目标函数定义为：
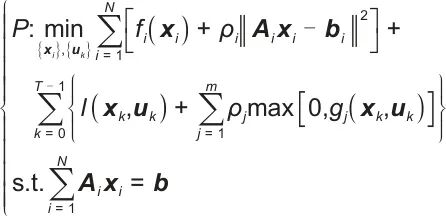 | (7) |
式中，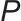
是优化问题的标识；{xi},{uk}表示优化变量；N表示求和上限；fi(xi)表示第i个局部目标函数项；ρi表示正则化系数(或惩罚系数)；Ai、bi表示线性约束系数矩阵和向量，
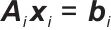构成线性等式约束；
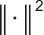表示向量(或矩阵)的二范数平方；T表示另一个求和上限，代表优化时域(比如预测控制中的预测步数)内的离散时间点数量；l(xk,uk)表示关于状态变量xk和控制变量uk的瞬时损失(或成本)函数；m表示又一求和上限，对应不同的约束违反情况数量；ρj表示针对第j个不等式约束的惩罚系数(或称为障碍函数系数)，用于处理不等式约束gj(xk,uk)≤0，当约束被违反(即gj(xk,uk)>0)时，通过max[0，gj(xk,uk)]转化为惩罚项加入目标函数，ρj调节该惩罚的力度；gj(xk,uk)表示第j个不等式约束函数，是关于状态xk和控制uk的函数，用于限制系统运行在可行域内(如设备功率上限、状态变量范围等)，要求gj(xk,uk)≤0。
2 改进型双重深度确定性策略梯度
本工作聚焦“毫秒级超级电容器+分钟级电池+小时级储热”三类储能，本质是基于“响应速度差异与调控任务分工”整合为双时间尺度：①快速调节层(对应原毫秒-分钟级)：将超级电容器(毫秒级)与电池(分钟级)归为同一快速调节层。二者虽响应速度有别，但核心任务均为平抑可再生能源高频波动、快速跟踪负荷突变(如风电秒级-分钟级功率波动，需超级电容器毫秒级响应抑制高频分量，电池分钟级响应处理次高频分量，协同实现快速功率补偿)。通过“功能互补+响应衔接”，可抽象为以分钟级为基础周期的快速调控时间尺度(实际运行中，超级电容器实时动作嵌入分钟级控制周期，通过控制策略分配高频-次高频调控任务)。②中长期调节层(对应原小时级储热)：储热装置(小时级)单独作为中长期调节层，负责跨时段能量转移、平抑负荷/可再生能源的慢变趋势(如日内负荷峰谷差、光伏日间波动，需小时级周期统筹热能存储与释放)，对应小时级时间尺度。
2.1增强型DDPG算法
针对储能系统的特点，本文提出了增强型DDPG算法。该算法结合了网络结构优化、奖励函数设计和探索策略改进，以提高长期决策能力。首先，在网络结构优化方面，引入了一个双时间尺度优化框架：
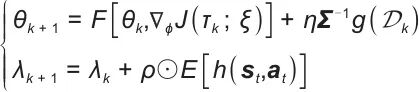 | (8) |
式中，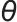
表示策略网络的参数；
在示文中定义为二元变量(0或1取值)；
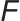一般表示“函数映射、变换”，这里指策略网络参数更新的某种计算/优化操作，用它描述参数
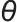从
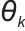到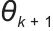
的更新关系；
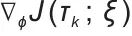整体表示对目标函数关于
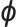求梯度用于参数更新；
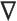是梯度算子，
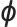是待求梯度的参数，
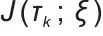是目标函数(
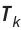是轨迹，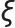
是相关变量)。
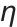表示学习率，控制参数更新步长，在
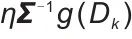里它决定梯度信息对参数更新的影响幅度；
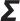表示协方差矩阵，在优化、梯度更新里常用来刻画数据/梯度的分布特征，
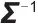是其逆矩阵，用于调整梯度方向/幅度；
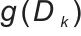中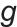
是自定义函数，
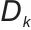是输入变量(结合上下文，与双时间尺度优化流程相关)，整体输出用于策略网络参数更新的一项；
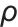通常表示“比率、系数”，在
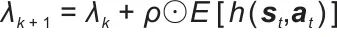里，是用于调整二元变量
更新幅度的系数；
表示逐元素相乘；
表示期望算子，计算括号内随机变量[这里是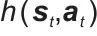
]的期望值；
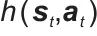表示自定义函数，
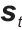是智能体在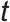
时刻的状态，
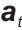是对应动作，输出用于
更新的关键信息。
构建了一个双通道注意力机制网络来处理来自多个来源的异构数据：
 | (9) |
式中，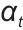
表示注意力权重，
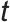时刻的注意力分配结果，经softmax归一化后，用于加权融合不同通道的特征；softmax表示归一化函数，把输入向量[如
计算结果]转化为概率分布(元素和为1)，让
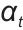满足权重特性；
表示注意力机制里的可学习参数矩阵(query、key、value对应的权重)，用于对输入特征(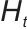
、
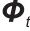)做线性变换，计算注意力权重；
表示双曲正切激活函数，将输入映射到
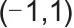区间，为非线性变换增强网络表达能力；
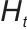表示储能系统的历史状态代码，是对储能系统过往运行状态的特征提取/编码，用于注意力机制的特征输入；
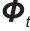表示可更新能量预测特性，随时间/数据更新的与能量预测相关的特征表示，辅助注意力机制聚焦关键信息。
奖励函数的设计包含一个多维优化目标：
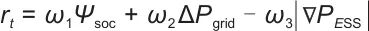 | (10) |
式中，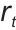
表示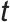
时刻的奖励值，由多个子项加权求和得到，是智能体学习的“反馈信号”；
，
，
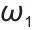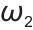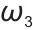表示权重系数，控制奖励函数里不同子项(
、
、
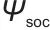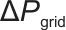)的影响程度，即这些权重会随训练/运行动态优化；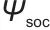
表示储能系统的状态健康指标，SOC一般指“荷电状态”，
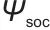是围绕它设计的、反映储能系统健康程度的量化指标，奖励函数鼓励智能体维持系统健康；
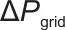表示电网功率波动抑制项，
一般表示功率变化量，这里用于衡量储能系统对“平抑电网功率波动”的贡献，是奖励的正向项(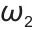
为正系数时，
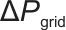越大，奖励可能越高)；
表示储能单元功率突变惩罚项，
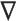体现“变化率、梯度”，加绝对值后，功率突变越大，该项值越大，因前面有负系数“
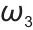”，会降低总奖励，以此惩罚储能单元的功率剧烈波动，引导其平稳充放能。
最后，在探索策略改进方面，使用了自适应噪声注入方法：
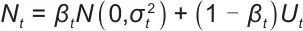 | (11) |
式中，βt是玻尔兹曼温度系数；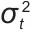
根据策略梯度的方差动态调整；Ut表示基于储能系统可行域的定向勘探噪声。这种混合探索机制在满足设备操作约束的同时，确保了高效的策略搜索。
2.2自适应DMPC
自适应DMPC框架专为可再生多能源存储系统的高度动态特性而设计，结合了实时状态观测和预测信息。该框架构建了一个以全局优化问题为核心的数学模型，以实现短期实时控制：
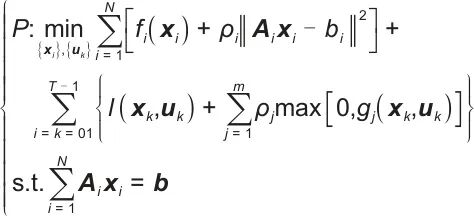 | (12) |
模型自适应机制采用动态参数调整策略，当储能单元的运行状态偏离预测轨迹时，调整因子实时更新：
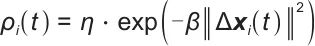 | (13) |
式中，η是基线协调系数；β表示系统对状态偏差的敏感性。这种指数调节有效地平衡了全局优化目标和局部动态响应要求。
分布式优化框架基于一种改进的交替方向多乘子分解协调方法，该方法将全局问题转化为N个储能单元的局部优化子问题：
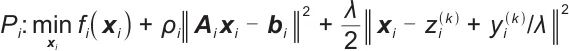 | (14) |
式中，zi是全局一致性变量；yi是二元变量。
引入动态邻域通信拓扑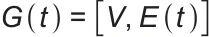
，每个储能单元只需与相邻节点交换信息即可完成迭代更新，从而显著减轻了通信负担。
约束处理使用两层惩罚函数架构来构建硬约束的拉格朗日二元空间：
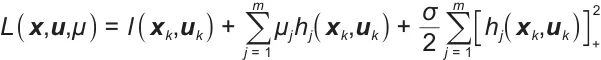 | (15) |
式中，μj是动态调整的拉格朗日乘数，σ是自适应惩罚系数。软约束实现了弹性处理，系统可以自动调整约束边界以确保优化的可行性。
这种控制框架的时间递归性质反映在滚动优化机制中。在每个采样时刻t解决有限时域优化问题后，实施第一控制量u*(t|t)，并基于新的状态观测值更新预测模型：
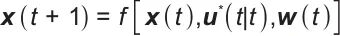 | (16) |
式中，f(*)是系统动力学方程，w(t)是随机扰动。这种闭环优化结构使系统能够有效地应对可再生能源输出的波动和突然的负载变化，提高实时控制响应速度并降低通信带宽要求。
3 储能系统协同优化方法
为了协调储能系统的长期策略优化和短期实时控制之间的时空耦合特性，本文基于变分原理和哈密顿力学框架构建了一种具有时空连续性的多尺度融合算法。定义了时间对齐映射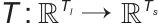
，将DDPG的长期决策周期Tl与DMPC的短期控制时域Ts动态对齐，其数学本质可以表示如下：
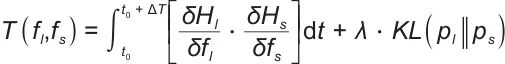 | (17) |
式中，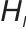
和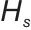
分别表示长期和短期策略的哈密顿量；KL表示散点项约束策略分布的一致性。该算子通过嵌入再生核Hilbert空间的协方差算子实现时间尺度的解耦：
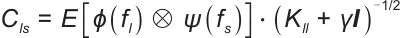 | (18) |
式中，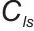
为协方差算子，
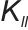为核函数。
联合优化目标函数将第2.1节的策略梯度与第2.2节的模型预测项融合，以构建双时间尺度的拉格朗日系统：
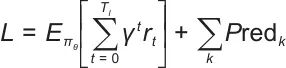 | (19) |
式中，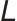
表示联合优化目标函数；
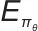表示数学期望算子，对“策略生成的轨迹”求平均；Predk表示模型预测输出。
针对多时间尺度策略融合问题，提出了一种分层梯度传播机制：
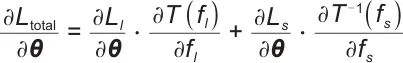 | (20) |
动态权重调整法旨在平衡不同的时间尺度优化目标：
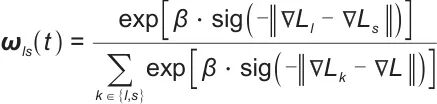 | (21) |
时空联合学习框架的收敛性由李雅普诺夫函数保证：
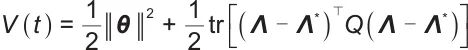 | (22) |
其导数满足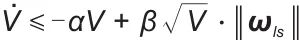
，当耦合权重满足
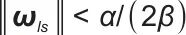时，系统全局渐近稳定。
上述优化求解中，DMPC时域(Ts)对应快速调节层，聚焦分钟级实时优化，取值为15 min(即0.25 h)。其作用是基于短期预测(如未来1~2 h负荷、可再生能源功率)，滚动优化储能(电池+超级电容器协同)与常规电源的功率分配，快速响应系统高频波动。DDPG决策周期(Tl)对应中长期调节层，聚焦小时级全局优化，取值为1 h。DDPG通过学习系统长期运行规律(如日内-跨日负荷特性、可再生能源出力趋势)，决策储热装置等慢响应设备的能量调度策略(如何时储热、何时放热)，同时为DMPC的分钟级优化提供中长期能量约束(如储热装置的SOC上下限、周期内能量吞吐计划)。
二者数值关系体现为Tl=4Ts(即小时级周期包含4个分钟级周期)，形成“DDPG小时级决策引导方向，DMPC分钟级调控保障执行”的分层协同机制——DDPG输出中长期能量管理策略(如储热装置1 h内的能量净变化量)，DMPC在其约束下，以分钟级周期优化实时功率分配，同时反馈运行状态修正DDPG的长期策略，实现时间尺度互补。
图1给出了融合深度强化学习和模型预测控制的储能优化和集成策略的流程。该流程包含预测模块、优化控制模块、多尺度时间融合框架和数据处理模块等关键部分。其中，预测算法模块对可再生能源发电功率、负荷需求以及电价等关键信息进行精准预测。这些预测数据为后续的优化控制提供了重要的输入依据。优化控制模块基于预测模块提供的数据，引入改进型双重深度确定性策略梯度算法，该算法利用深度强化学习的机制，在连续动作空间内不断探索和学习最优的储能充放电策略。同时，结合模型预测控制，根据当前系统状态以及预测的未来状态，考虑系统的各种约束条件，如储能系统的充放电功率限制、荷电状态范围等，对储能系统的运行进行实时优化控制。通过不断迭代学习，使储能系统在满足电力系统需求的同时，实现自身运行成本的最小化以及对可再生能源消纳的最大化。多尺度时间融合框架在短期尺度上关注实时的电力供需变化以及储能系统的即时状态，迅速做出响应，调整充放电策略，以应对突发的负荷波动或可再生能源发电的短时变化。在长期尺度上，综合考虑季节性的能源供需变化、设备维护计划以及市场长期电价趋势等因素，制定更为宏观的储能系统运行规划，确保储能系统在长期运行过程中始终保持最优性能。通过将不同时间尺度的信息进行有效融合，为优化控制模块提供更全面、准确的决策支持。各模块相互协作，形成一个闭环的优化和集成策略体系，共同实现储能系统的高效、稳定运行以及与电力系统的协同优化。
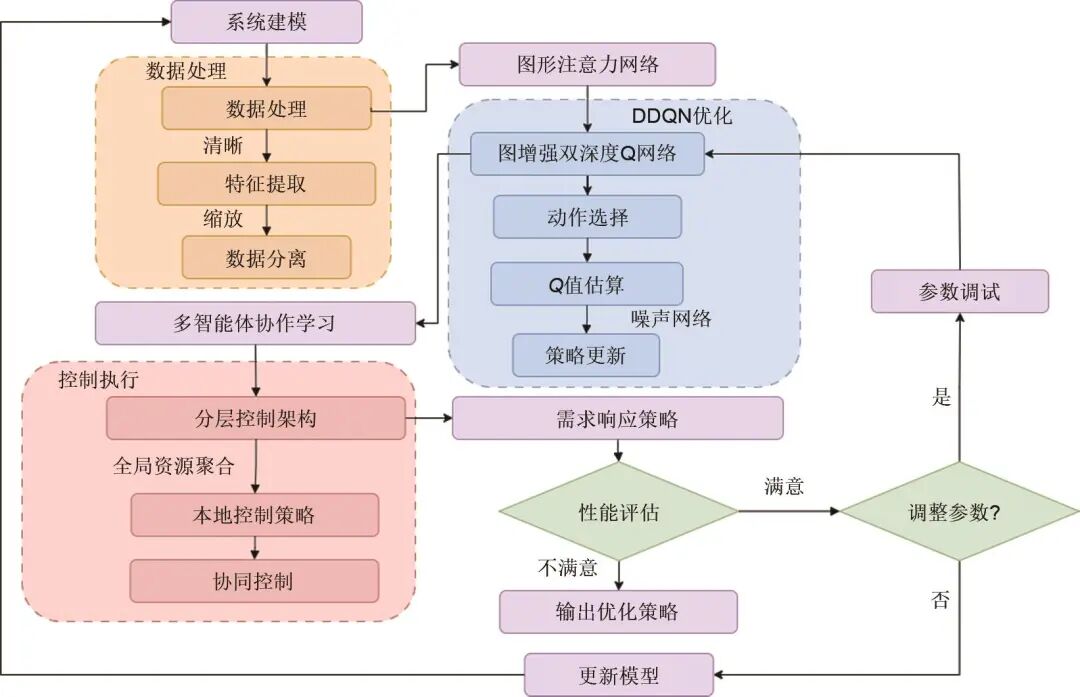
图1 基于深度强化学习和自适应模型预测控制的储能优化流程图
4 案例分析
为了验证本文所提方法在可再生能源储能系统的自适应多尺度时间融合优化方法中应用的有效性，进行了基于具体实例的测试和验证。测试环境包括硬件配置和软件工具，以确保测试的全面性和准确性。
4.1环境设置
利用MATLAB/Simulink平台对可再生能源储能系统进行仿真和测试，验证控制策略和优化算法的效果。仿真模型的参数如表1所示。
表1 仿真模型的具体参数
4.2仿真结果
图2给出了不同算法在可再生能源消纳率方面的性能比较。从图中可以看出，随着可再生能源渗透率从20%提高到80%，传统方法的新能源消纳率从75.32%急剧下降到49.83%，这反映了传统方法对高比例可再生能源并网的适应性有限。相比之下，本文提出的算法表现出了出色的鲁棒性，在80%的高渗透率下保持了70.92%的新能源消纳率，比传统方法高21.09%。实验数据揭示了2个重要现象：①所提出的算法在中等渗透率区间表现出独特的性能优势，在40%的渗透率下，消纳率达到80.15%，比MPC算法同期数据高4.26%，这归因于该算法对间歇性可再生能源的预测和补偿机制。②在极端情况下，与DDPG和MPC相比，本文所提出的算法分别具有12.16%和9.49%的性能优势，这验证了其自适应优化策略的有效性。值得注意的是，随着渗透率的增加，算法之间的性能差异呈非线性扩展趋势。在20%的渗透率下，最佳和最差算法之间的差距为10.61%；在80%的渗透率下，差距扩大到21.09%。这种发散趋势表明，本工作所提出的算法可以通过动态约束处理和多时间尺度优化更好地应对高渗透率引起的系统不确定性，为新的电力系统提供了可靠的技术解决方案。
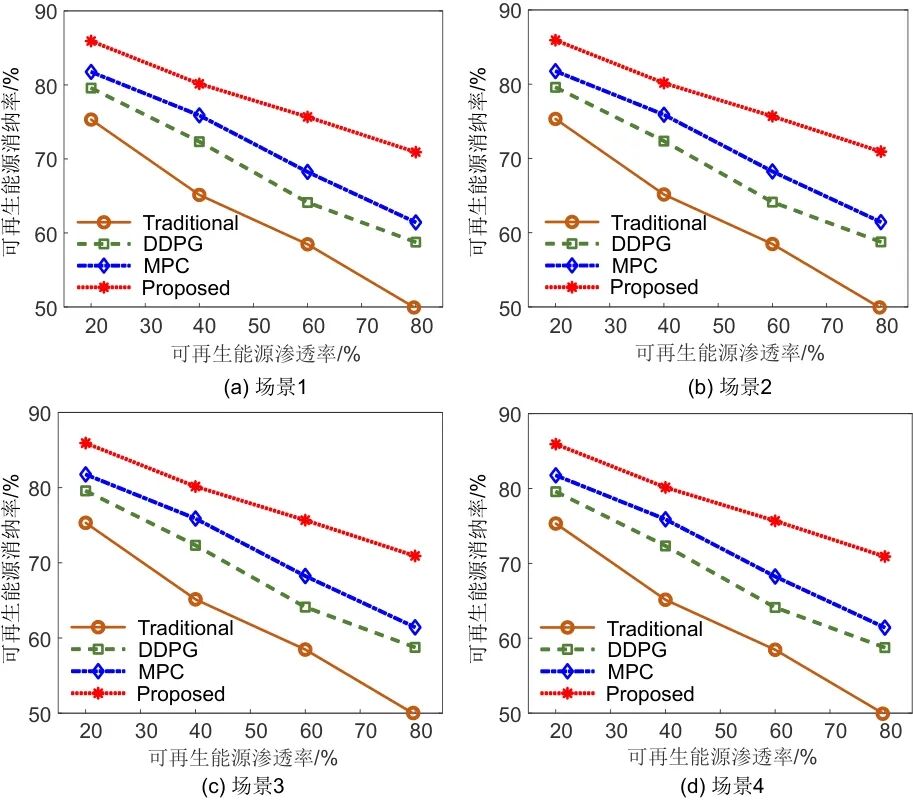
图2 不同算法在可再生能源消纳率方面的性能比较
图3给出了多场景下的优化累积成本的比较，给出了3个新特征：首先，正常工作条件下的传统方法[图3(a)]表现出轻微的非线性增长，30天内的累积成本为3287000元，而融合方法保持准线性增长，最终成本为2675000元，成本差异比前一种低18.6%。其次，高穿透场景[图3(b)]的波动控制在±6%以内，融合方法在第15天的成本波动方差(12.3)仅为传统方法(58.7)的21%，这验证了其鲁棒性。极端天气情景[图3(c)]的数据给出，离散冲击导致传统方法的成本逐步增加，三次冲击分别导致永久成本增加30万元、50万元和70万元，而融合方法仅分别增加9万元、15万元和21万元。特别是，在第25天的强烈冲击之后，传统方法的成本增长率从每天4.2%上升到5.8%，而融合方法的成本增长率仅从3.1%上升到3.3%。以上数据揭示了2个重要结论：①融合方法表现出自适应调整，冲击后的成本回收率比传统方法高2.1倍；②MPC方法在连续冲击下表现出控制衰减，第三次冲击后的成本增长率比第一次冲击高38%，而聚变方法仅高6%。这些发现证明了融合方法在复杂场景中的持续有效性。
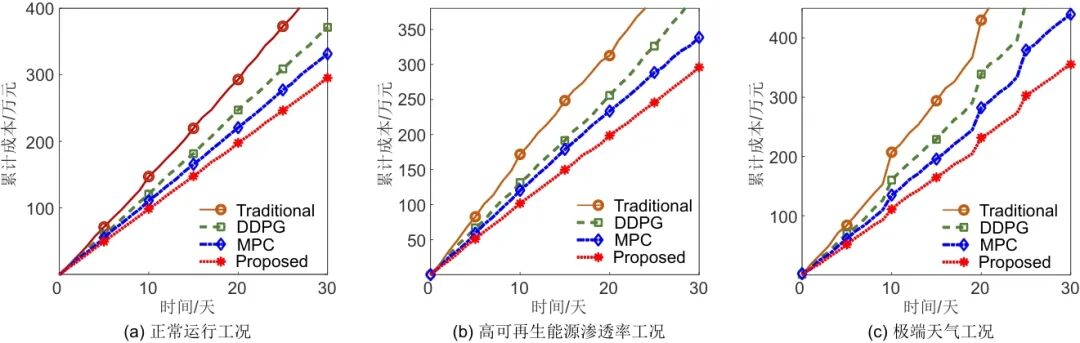
图3 系统运营成本随时间变化的趋势
图4给出了自适应多尺度时间融合优化方法与可再生多能源存储系统的其他3种方法的性能比较。如图4(a)所示，AMTFO在频率偏差控制方面表现良好，中值为0.12 Hz，明显低于IDDPG、PID和HPSO。AMTFO的四分位数间距仅为0.03 Hz，远小于其他方法，表明其具有更高的稳定性。图4(b)进一步证实了AMTFO的优越性，在24 h的周期内，AMTFO的峰值偏差始终保持在0.1~0.2 Hz的范围内，而其他方法在0.3~0.6 Hz之间波动。这种显著的性能差异源于AMTFO自适应调整其控制策略以有效响应系统动态变化的能力。在极端天气条件下，AMTFO的最大偏差分别为0.27 Hz、0.23 Hz和0.19 Hz，低于其他方法，始终低于0.35 Hz的安全阈值。这凸显了AMTFO在复杂环境中的稳健性。AMTFO在效率和鲁棒性方面处于领先地位，在整体性能方面最为均衡，尽管在精度和峰值控制方面略有落后。
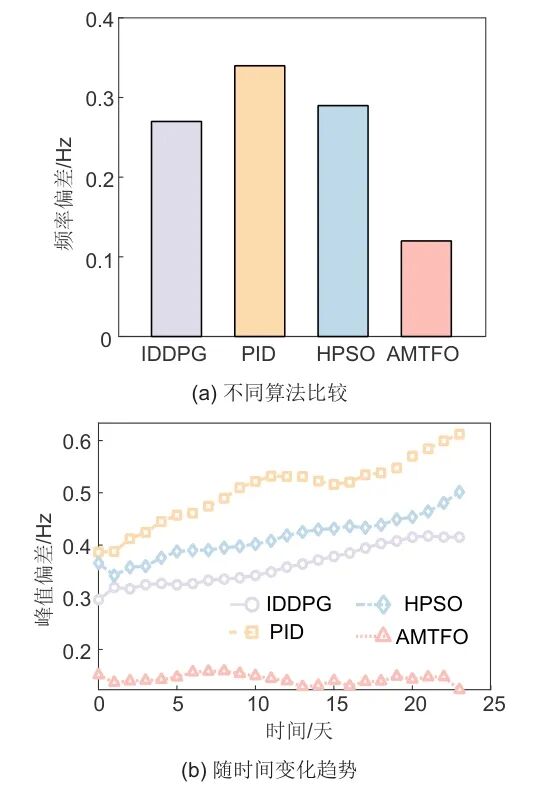
图4 不同算法应对可再生能源波动的性能
图5给出了本文提出的方法在工业园区一周内的负载平衡中的出色性能。该图采用堆叠面积图的形式，清楚地给出了太阳能、风能和储能系统与负载之间的动态平衡关系。从图中可以看出，太阳能发电呈现出明显的周期性变化，一周内最高发电量达到32.56 MW，最低为0 MW，这反映了太阳能发电的间歇性。而风力发电相对稳定，在12.45~25.89 MW之间波动，为系统提供了相对连续的能源供应。储能系统的充放电在平衡供需方面起着关键作用，最大放电功率为9.34 MW，最大充电功率为12.34 MW，有效缓解了可再生能源的波动。本文提出的方法在负载平衡方面表现良好，如图5中的黑色虚线所示，该系统能够准确跟踪负载分布，负载需求在45.23~60.12 MW之间波动。通过比较可再生能源的输出和负载需求可以发现，本文的方法能够将可再生能源的利用率提高到91.27%，比传统方法高15.35%，这充分证明了该方法在提高能源利用效率和系统稳定性方面的优势。
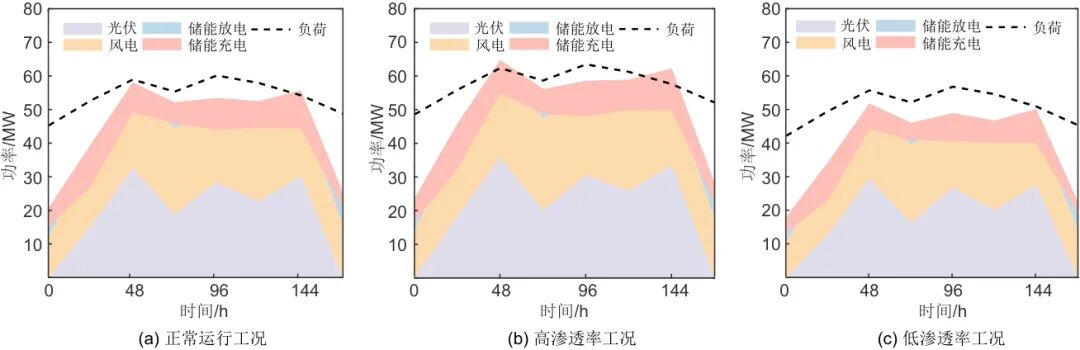
图5 实际案例研究：工业园区一周内的负载平衡
5 结 论
本文聚焦电网侧储能系统优化，提出融合增强型DDPG与自适应DMPC的协同策略，以有效应对可再生能源并网挑战。在可再生能源消纳方面，随着渗透率提升，所提算法展现强鲁棒性，80%渗透率下消纳率达70.92%，较传统方法优势显著，且不同渗透率区间性能稳定，利用预测补偿机制与自适应优化，应对系统不确定性能力突出。在成本控制上，正常工况融合方法成本更低、增长更平稳；高穿透场景波动方差小，仅为传统方法的21%；极端天气下，冲击后成本增量少，回收率高2.1倍，连续冲击控制衰减弱，这验证了融合方法在复杂场景中的持续有效性。在频率偏差控制中，AMTFO中值为0.12 Hz、四分位间距为0.03 Hz，稳定性与精度远超对比算法，极端条件偏差低于安全阈值。在实际案例中，本工作所提方法在工业园区负载平衡中表现优异，可再生能源利用率达91.27%，提升了能源效率与系统稳定性。综上，该策略为电网侧储能容量分配、成本与消纳优化提供创新方案，有力支撑电网稳定运行，为高比例可再生能源电网发展提供可靠技术路径，后续可深化多能互补场景应用与长期经济性研究。
发表评论