百MWh级竖井式重力储能系统重物块储存与运输方案

作者：曾小超 1 姜健宁 1李建文 2 管春宝 2

单位：1. 中国电力工程顾问集团华北电力设计院有限公司 2. 新能源电力系统国家重点实验室(华北电力大学)

引用本文：曾小超, 姜健宁, 李建文, 等. 百MWh级竖井式重力储能系统重物块储存与运输方案[J]. 储能科学与技术, 2025, 14(10): 3839-3847.

DOI：10.19799/j.cnki.2095-4239.2025.0196

本文亮点：针对重力储能重物块数量多、功率间歇性大的问题，提出了考虑重物块分级储存与最优路径运输的方案；运用迪杰斯特拉（Dijkstra）算法对重物块的选择及运输路径进行了优化规划。

摘 要 大容量竖井式重力储能系统是实现长时储能的有效手段，在考虑利用电机暂态支撑特性需直接并网的应用背景下，重物块分级是竖井式重力储能系统灵活调节功率的可行方法。但MW级百吨重物块储能系统功率间歇性大，百MWh容量的重力储能系统重物块数量多，重物块如何分级、如何储存与运输是其系统运行亟须解决的关键性问题。本研究针对上述问题，提出了考虑重物块分级储存与最优路径运输的方案：首先，根据电池组可调最高功率及储能限额将重物块质量分为四个等级，由典型日光照时长确定各级总块数，以空间最大化设计了其储存区域，在此基础上，考虑重物块运输时间、块数的约束条件，利用迪杰斯特拉(Dijkstra)算法对重物块的运输路径进行了规划，以实现运输路径最短；然后，对重物块总储存区进行分区并采用四辆自动导引车(automated guided vehicle，AGV)协同运输，推导了AGV所需的最小加速度，以确保运输过程的效率；最后，通过典型日净负荷功率波动平抑算例，验证了百兆瓦时重力储能系统重物储存及运输的有效性。

关键词 重力储能；质量分级；存储分区；路径规划

长时储能技术将通过其跨日、跨月乃至跨季节的充放电循环能力为以新能源为主体的新型电力系统提供必要的长期稳定的“削峰填谷”调节能力。大容量竖井式重力储能技术作为实现长时储能的有效手段之一，具有选址灵活、环境友好、储能容量大、循环寿命长、零自放电率、放电深度高、响应快和效率高等优点，应用前景广泛。近日，全球首个竖井式重力储能工程化应用项目落户中国河北省赤城县，该项目由中国电力工程顾问集团及下属华北电力设计院共同投资建设，现场进行深部地质勘探的单个钻孔突破1000米深度大关，其单机功率为16 MW，预计2025年内并网发电，这标志着竖井式重力储能技术取得了显著进展。

大质量的重物块存在输出功率间歇性过大的问题，无法实现功率的柔性输出，目前研究多集中在混合储能优势互补或者多机协调控制与调速上。苏格兰Gravitricity公司设计的地下竖井式重力储能系统可以控制重物下落速度改变发电时间和发电功率。Tong等介绍了一种创新容量配置策略，即相等容量配置和双倍速率容量配置来优化储能效率和稳定性。中国科学院电工研究所提出了基于多电机集群或耦合功率型飞轮储能系统的协调控制策略，以提升系统的稳定性、能效及电能质量。国网智研院和文献[9]提出了重力储能耦合超级电容器储能的技术方案，对混合储能系统进行功率平滑控制，并通过多机组运行时序配合实现功率平滑。可见，单机系统可以采用变频调速与重物块分级的方法，但采用电机变频调速需要变频器与电网连接，其利用电机惯量和阻尼特性来增强系统稳定性的优势无法体现，因此，电机定子侧直接并网，采用重物块分级运行控制，是既利用电机自身优势又满足多级功率的有效手段。然而，目前针对大容量重力储能单元的重物块分级平滑功率输出的研究相对较少。

百MWh重力储能系统重物块数量繁多，如何规划储存位置及最优运输路径是保证重力储能系统运行效率的一个关键性问题。传统的最短路径算法主要有弗洛伊德(Floyd)算法和迪杰斯特拉(Dijkstra)算法，其中，Floyd算法是解决多源最短路径问题的经典方法，适用于需要计算图中所有顶点对之间最短路径的情况，不适用于解决单源节点最优路径规划的问题。而Dijkstra算法是一种典型的用于解决单源最短路径问题的高效算法，文献[12]研究并应用该算法实现了仓库最优的单车及多车路径规划。文献[13]在考虑能耗的基础上改进该算法，实现了单AGV及多AGV系统的路径规划，提升了效率，降低了运营成本。文献[14]运用拓扑地图法对AGV车间运行环境构建有向电子地图，并运用Dijkstra最短路径规划算法对有向电子地图中的各个节点进行最短路径规划。文献[15]提出了一种基于Dijkstra算法的自动代客泊车系统抗拥塞路径规划方案，可以根据用户的选择和需要提供最优的服务路径，并以最短、最快的路线到达目标位置。文献[16]针对工厂内物流运输AGV的路径规划效率等问题，提出一种将Dijkstra算法存储方式变更为邻接表，并通过二叉堆存储未扩展结点的存储模型,实现了数据结构上对邻接结点搜索的优化。可见，Dijkstra算法具有一定的灵活性和稳定性并且具有较低的时间复杂度，这使得Dijkstra算法能在物流配送、自动泊车和地图导航等方面应用，因此本工作利用Dijkstra算法对重物块进行最优路径规划。

1 工程背景

以全球首个竖井式重力储能工程化应用项目为例，16 MW竖井式重力储能系统主要包括重物块、AGV、轿厢、竖井、巷道、地面平台和井底平台、上下层轨道、支撑架、滑轮、电机等部件。系统上下层储存区为平行的相同结构，AGV为水平转移重物块载体，系统通过轿厢实现重物块在高低平台间的升降，并通过电机完成机械能和电能之间的相互转化。工程中，地下竖井深可达1000 m，重物块最大质量为104 t，其系统基本结构如图1所示。

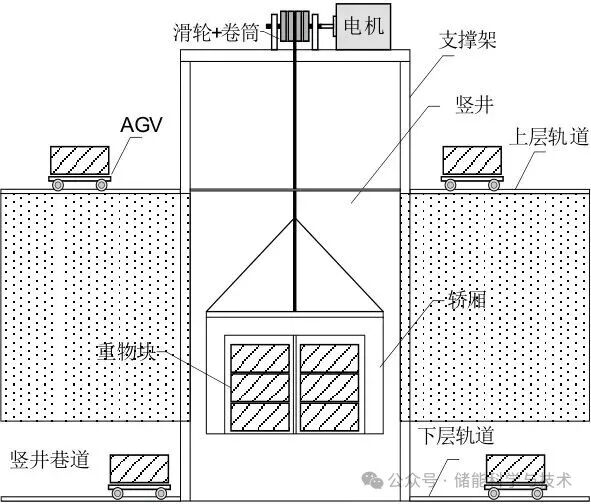
图1   重力储能系统示意图

2 重力储能系统重物块储存设计

2.1根据功率响应确定重物块分级标准

在众多储能技术中，电化学储能技术具有较高的技术成熟度。通过对多家电化学储能单元调研对比，比亚迪储能CS20H-B2982-A-R1M01型电池储能系统为最大单元输出功率，约为2700 kW。基于此，设计重物块最小质量等级能够满足额定速度下运行时，输出功率设定为2700 kW，更精细的功率响应可由混合储能优势互补完成。对于中间等级的重物块，每个质量块都是前一个的两倍，使得系统可根据电网功率需求灵活选择不同等级的重物块。设重物块形状为正方体，材料为混凝土(2500 kg/m³)，具体重物块分级边长、质量及对应输出功率如表1所示。

表1   重物块质量分级及其参数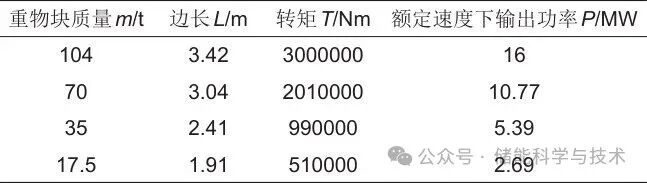

2.2根据能量需求布局四级重物块储存位置

在设计重力储能系统时，考虑到超短期预测的最短时间间隔为15 min，重力储能系统应能够满足该时间段的能量需求。因此，四质量等级重物块设计为一组，每组重物块需要满足15 min内的新能源与负荷预测差值的需求。据统计，张家口近三年夏至日(6月20日或21日)的最长光照时长记录为15 h 6 min左右，即最长光照时间不会超过16 h，需要重物块64组即每级重物块均为64块，以满足电网日内调度的灵活性及削峰填谷能力的需求。同时，为了确保整个重力储能系统能够达到百兆瓦时的容量需求，将104 t重物块的数量设为374块，进而得到四级重物块块数及单个储存方格边长见表2。

表2   四级重物块块数及单个储存方格边长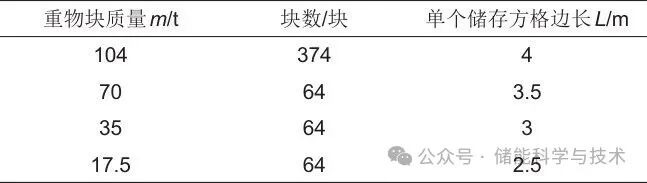

为方便重物块的运输和管理，以“田”字形储存区域分别对不同质量等级的重物块进行储存，其中中心交汇处为矿井位置，该方案中此处放置四台电机。方格处为重物块储存区，根据表2中各级重物块尺寸，每个储存区设计为边长44 m的正方形，其余部分为宽8 m的运输道路，如图2所示。左上区域为104 t重物块储存区，共可储存121块；此布局为其他质量等级重物块的储存提供了模板，通过按比例调整储存区的尺寸，确保其他质量等级的各64块重物块紧邻矿井侧，以实现快速调运；剩余空间储存104 t重物块，以实现空间的最大化利用。

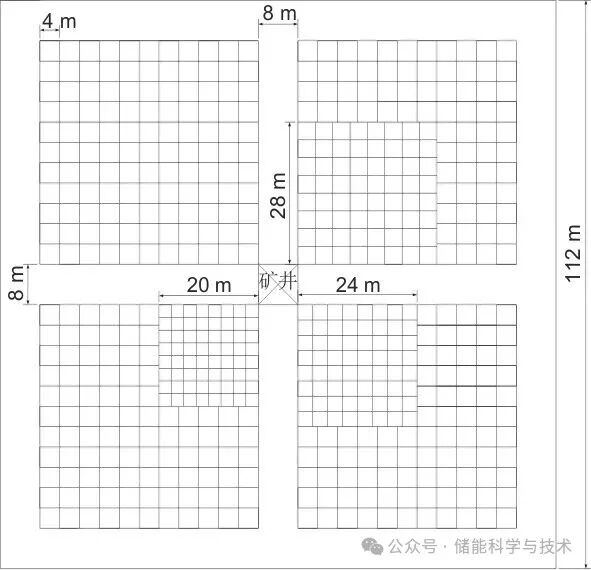
图2   重力储能系统总储存区示意图

3 重力储能系统重物块运输设计

3.1运输条件约束

3.1.1 运输时间约束

重物块在竖井中运行时需要经过加速过程、匀速过程和减速过程三个过程，当重物块运行达到额定速度时，电机达到额定功率，以两个重物块为例重力储能系统重物块具体运行示意图见图3。

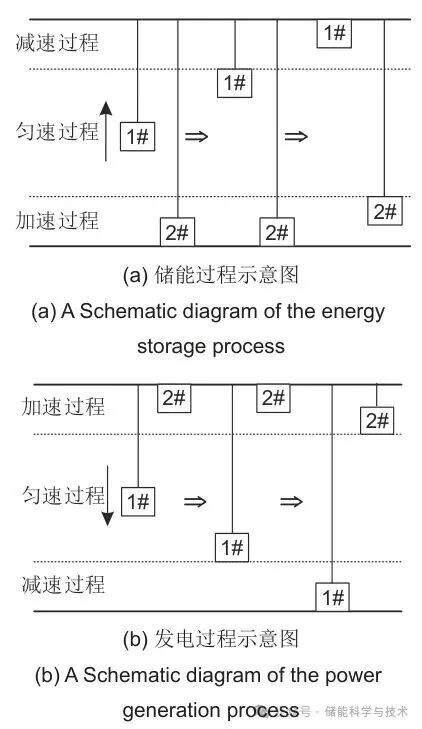
图3   重力储能系统重物块运行示意图

在储能过程图3(a)中，第一阶段由1#重物块加速和匀速运行，2#重物块处于待机状态；第二阶段当1#重物块即将运行到减速过程时，2#重物块开始加速运行；第三阶段1#重物块停止运行，2#重物块完成加速并即将进入匀速过程。两个重物块通过时序配合、容量和速度匹配，储能容量增大且功率平滑。在发电过程中两机重物块运行规律相同，如图3(b)所示。

根据电机的额定功率与重物块的质量，可求得重物块在竖井中匀速运行的速度：

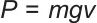(1)

其中，P为电机的功率，m为重物块质量，g为重力加速度。考虑到电机起动、制动的时间过短可能导致起动电流过大，从而对电机和电网造成冲击，影响电机的使用寿命，启动、制动的时间过长则会导致电机绕组过热，加速绝缘老化，因此设定电机启动、制动的时间为10 s左右，具体求得重物块在竖井中运行的所有参数如表3所示。

表3   重物块运行参数

设AGV每次装卸重物块所用的时间分别为t_装和t_卸，往返运输的总时间为t_运。在上述储能过程中以一辆AGV运输重物块为例，在1#重物块完成加速过程和匀速过程的时间内，AGV应完成2#重物块的运输和装卸，发电过程同理。由此可以得出AGV运输过程的时间约束为：

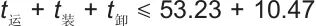(2)

3.1.2 运输块数约束

通过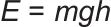可求得每块104 t重物块所储存的能量约为1.02×10⁹ J，换算后约为0.283 MWh。同理可求得70 t、35 t和17.5 t重物块所储存的能量分别为0.1905 MWh、0.0953 MWh和0.0476 MWh。以储能过程为例，假设重力储能系统需要储存的能量为E_储(MWh)，光伏系统发出的能量为E_光，负荷需求为E_L，则有：

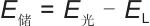(3)

设所需104 t、70 t、35 t和17.5 t重物块的个数分别为a、b、c、d，[x]为取整函数，则

(4)

即总重物块数量

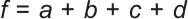(5)

在重物块总块数在最小的约束条件下，向下取整即可以求得每次日内调度所需各个质量等级重物块的个数，发电过程同理。

3.1.3 运输距离约束

在矿井重物块的运输优化问题中，面临着从起点(矿井位置)到终点(每个储存方格位置)的最短路径规划问题，本工作采用Dijkstra算法来解决这个问题，在路径规划的过程中，考虑现有的运输网络，并识别出那些因存储重物块而形成的障碍区域。通过规避这些区域，算法能够生成一条避开障碍物的最优路径。一旦确定了最优路径，便能够计算出运输车辆在该路径上所需的总运输距离，记为变量x。这个距离值x将作为AGV运输距离的约束条件。

将每一个储存方格中心都看成是一个储存点并进行编号处理，见图4，Dijkstra算法流程图如图5所示，其具体的执行步骤如下：

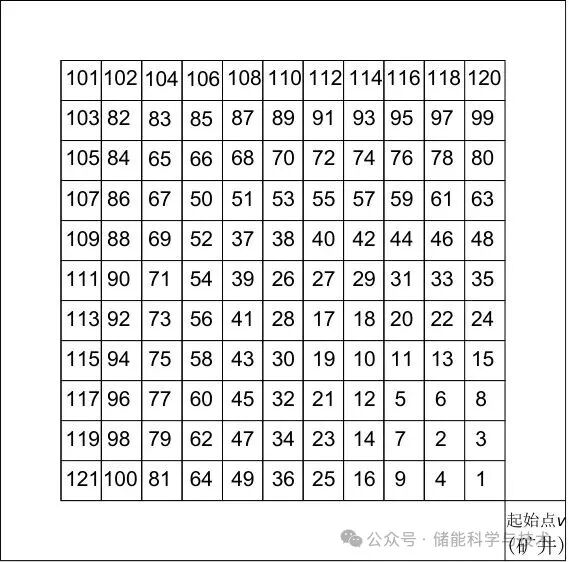
图4   重物块储存顺序编号

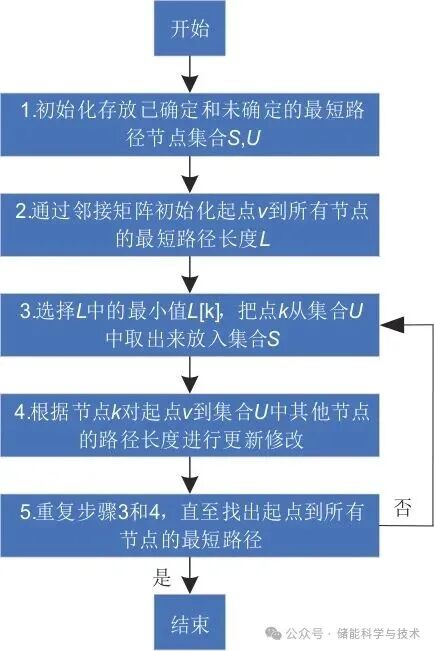
图5   Dijkstra算法流程图

（1）初始化阶段：初始时，集合S(已知距矿井最短距离的点的集合)仅包含起始节点v(矿井)，将其距离值设置为0；集合U(未知距矿井最短距离的点的集合)包含图中除v之外的所有储存点。对于v与U中任意储存点u之间若直接相连，则其权重为矿井中心与该储存点中心之间的距离；若u不是v的邻接点，则将u到v的边的权重视为无穷大。

（2）选择最小距离顶点：从集合U中选取一个距离起始节点v最近的储存点k，并将储存点k移至集合S中。此时，储存点k的距离值即为从起始节点v到储存点k的最短路径长度L[k]。

（3）更新距离估计：以储存点k为新的中间节点，遍历集合U中的所有储存点。对于每个储存点u，计算通过储存点k的路径长度，即储存点k的距离值加(k,u)的权重。若此路径长度小于储存点u当前记录的距离值，则更新储存点u的距离值为新的路径长度。

（4）迭代过程：重复执行步骤2和步骤3，直至集合U中的所有储存点均被纳入集合S中。此过程确保每个储存点的距离值反映从起始节点v出发的最短路径长度。

通过这一迭代过程，Dijkstra算法逐步构建出从起始节点到图中所有其他储存点的最短路径树，直至所有储存点的最短路径被确定。

3.2AGV运行区域划分及加速度设计

在AGV运行过程中，通过调研得知重载AGV运行的最大速度可以达到1 m/s。由于重载AGV运行速度低，仅一辆AGV无法在时间约束下完成重物块的运输任，需4辆AGV协调运行的方式，使其与4台电机一一对应。再次对重力储能系统总储存区进行分区处理，使每一辆AGV负责运输相应区域的重物块，具体分区情况如图6所示。对于对角线处重物块，根据相邻两个区域的运输车运行的情况，处于空闲的AGV来完成运输任务。

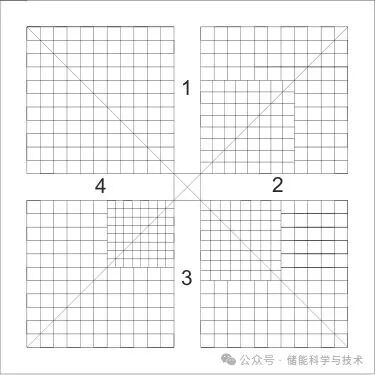
图6   AGV运输分区图

假设每辆AGV加、减速度大小为a，加、减速运行的时间为t₁，加、减速度运行的距离为x₁，匀速运行的时间为t₂，匀速运行的距离为x₂。以上述时间约束为参考，当4辆AGV共同运行时，每辆AGV的运输时间都会得到加长，具体情况如图7所示，4台电机通过时序配合依次运行的过程为：首先1#电机启动，经过加速、匀速和减速三个阶段，在1#电机减速时2#电机开始加速运行，以保证输出功率的平滑，同理当2#电机减速运行时，3#电机起动加速，以此类推。对于1#电机的卸载重物块、空轿厢运行及重物块重新装载过程，需在4#电机减速运行时，1#电机第二次开始运行前完成。由此约束供给1#电机的AGV运输过程时间。此时每辆AGV运输的时间约束为：

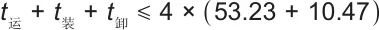(6)

图7   电机协调运行示意图

在重物块运输过程中存在直角转弯的情况，由于AGV载重量大，以一定的速度转弯可能会发生侧翻的危险，故采用定点回转的方式进行转弯，故AGV的运行过程为从矿井处开始加速到额定速度，随后匀速运行一段时间后到直角转弯处速度减为0，待定点回转完成后重新以相同方式运行。设重载AGV回转一周所需的时间约为40 s，假设装卸重物块的时间仍为10 s，最终得到AGV单程运输的时间t_运≤122.4 s，以运输距离最远的101号位置为例(图8)，此时AGV需要运行的单程距离为90 m，AGV定点直角转弯所需的时间为10 s，故AGV的直线运输时间为112.4 s。由于总运输时间的约束，以AGV直角转弯前后的路程比例将总运输时间进行分配，即运输距离越长分配到的运输时间也越长。101号位置在定点回转前后的运输距离分别为46 m和44 m，因此分配的运输时间分别为57.45 s和54.95 s。根据运动学公式即可求得AGV运行的最小加速度需求。对其单程定点回转前后运输过程分析如下：

图8   第101号位置运输路径

定点回转前

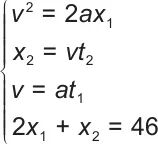(7)

时间上的约束条件为

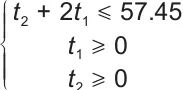(8)

最终求得AGV定点回转前加、减速所需要的时间t₁≤11.45 s，最小加、减速度为0.087 m/s²。同理求得AGV定点回转后加、减速所需要的时间t₁≤10.95 s，最小加、减速度大小为0.091 m/s²。因此，只需设定AGV直角转弯前后的运输时间分别为57.45 s和54.95 s，最小加、减速度大小为0.091 m/s²即可完成重物块的运输任务。

4 重力储能系统重物块储存与运输算例

以张家口市某地中午12：00—13：00的净负荷功率波动曲线(图9)为例，12：00—12：15时间段内净负荷为负表明负荷的需求小于发出的能量，此时重力储能系统应该储能，通过计算近似得到该15 min需要储存的能量约为2.12 MWh，据此计算出该时间段所需各等级重物块的个数，104 t重物块7块，35 t重物块1块。假设重力储能系统上层储存区在初始的重物块储存情况如图10所示，12：00—12：15这段时间内重物块需要储存的位置顺序及重物块储存后的情况如图11所示。

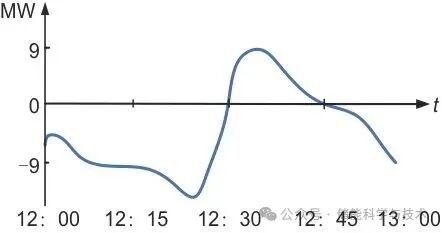
图9   张家口市某地典型日净负荷功率曲线

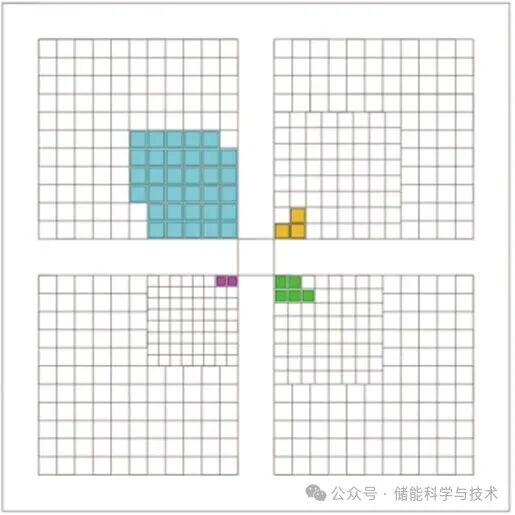
图10   上层储存区初始储存情况

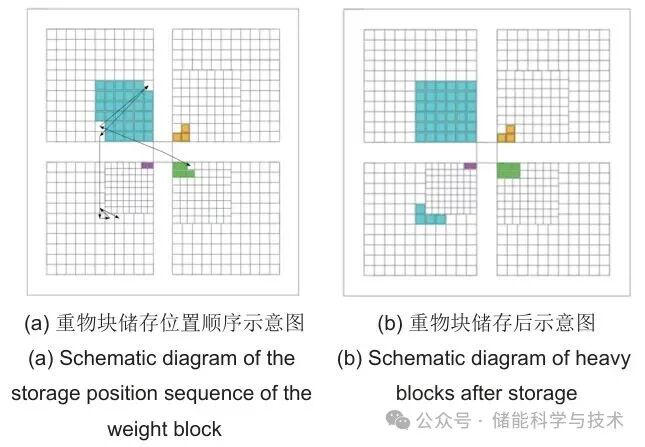
图11   12：00—12：15重物块储存示意图

同理，可以近似求得12：15—12：30需要储存的能量约为2.55 MWh，对应重物块质量等级和个数为104 t重物块9块，该段时间内重物块需要储存的位置顺序及重物块储存后的情况如图12所示。

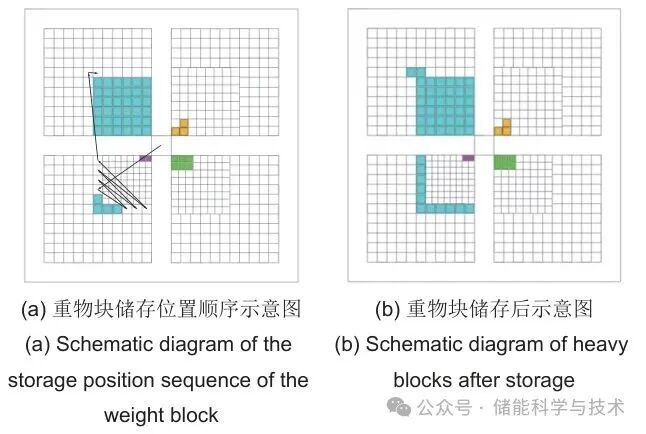
图12   12：15—12：30重物块储存示意图

在12：30—12：45时间段内，系统需要取出重物块以释放能量，在取出重物块时，以距离矿井远近为原则，从距离矿井最近的位置依次开始取出并运输重物块直至将需要的块数全部运输，12：30—12：45需要释放的能量约为1.04 MWh，对应重物块质量等级和个数为104 t重物块3块，70 t重物块1块，12：30—12：45时间段内重物块需要取出的位置顺序及重物块取出后的情况如图13所示。

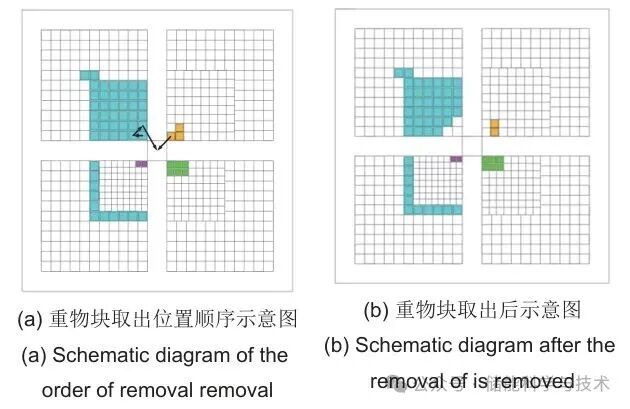
图13   12：30—12：45重物块取出示意图

在12：45—13：00时间段内，系统需要继续储存重物块，由于在上一个时间段上层储存区有重物块取出而导致矿井附近出现无重物块储存的情况，所以在后续重物块需要再次储存和运输时应先填补空缺位置，空缺填补后再重新进行后续的储存与运输，12：45—13：00需要储存的能量约为1.34 MWh，对应重物块质量等级和个数为104 t重物块4块，70 t重物块1块。12：45—13：00时间段内重物块需要储存的位置顺序及重物块储存后的情况如图14所示。

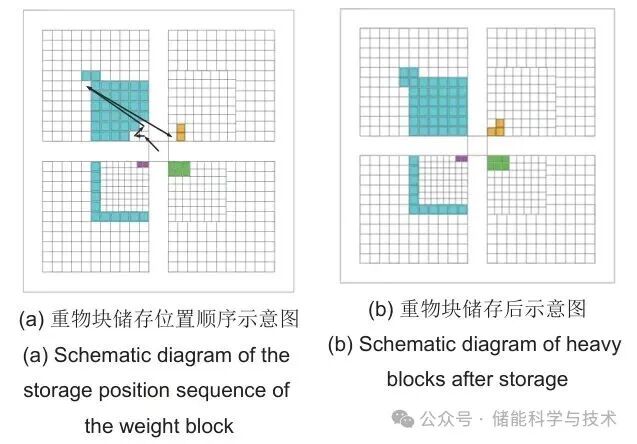
图14   12：45—13：00重物块储存示意图

在上述1小时的时间内，每个时段需求的能量和重力储能系统可以达成的能量对比图如图15所示，通过计算得到重力储能系统运行过程中的最大误差为1.3%。

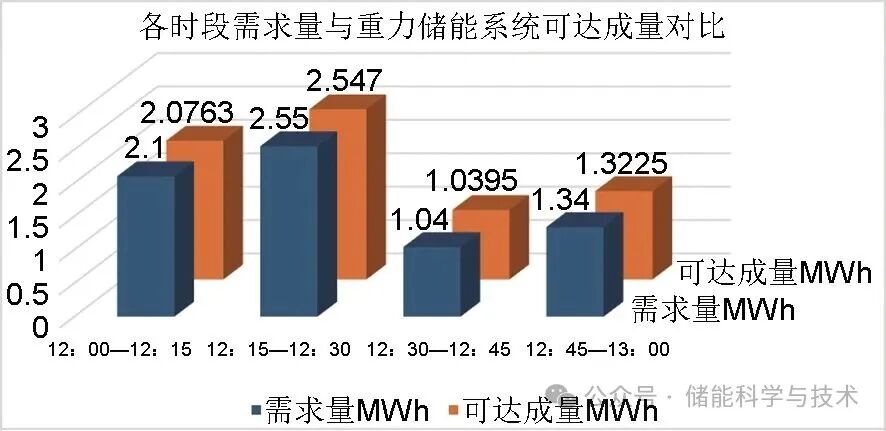
图15   各时段需求量与重力储能系统可达成量对比

5 不同负载转矩下，重力储能运行性能分析

重力储能系统通过调整重物块的级数即改变负载转矩，实现与电网调功需求的精准匹配，灵活平抑功率波动。通过对四级重物块发电与储能8种运行工况对发电电动机进行底层控制仿真，运行结果如表4所示，可见，随着重物块质量降低网侧谐波总畸变率降低、机侧谐波总畸变率增加，表明重物块分级调节功率方法对网侧较友好，而对电机耐谐波能力要求提高。

表4   转矩分级仿真结果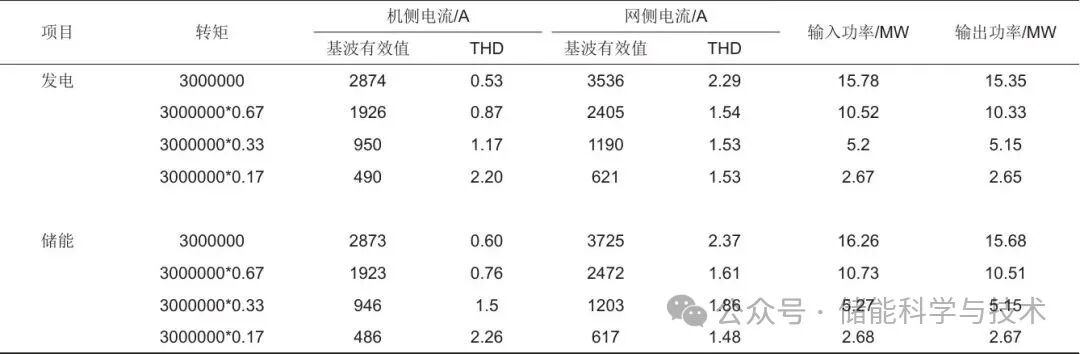

6 结论

本研究针对兆瓦级竖井式重力储能系统面临的重物块质量庞大造成输出功率波动性显著的问题，提出一种重物块质量分级、储存及运输方法。将电化学储能的最高功率等级确定为重力储能系统的最低输出功率等级，重物块分为17.5 t、35 t、70 t和104 t四级，并以“田”字形储存区域实现空间利用最大化。进一步提出总储存区分为四区、选用四辆AGV匹配四台电机的运输方案，综合时间限制和数量限制，利用Dijkstra算法对AGV的最短运输路径规划，在考虑AGV直角转弯的情况下，按定点回转前后运输距离的比例重新分配总时间，得到最远距离下定点回转前后的运输时间分别为57.45 s和54.95 s，依此推导出AGV所需的最小加、减速度为0.091 m/s²，确保了运输的可靠性。通过典型日净负荷功率波动平抑算例，验证了该方案的可行性和有效性。

第一作者：曾小超（1970—），男，本科，正高级工程师，从事重力储能应用技术；

通讯作者：李建文，副教授，从事重力储能技术及应用。